Pritha Bhandari 2023-06-21
描述性统计用于汇总和整理数据集的特征。数据集是从样本或整个总体中收集到的一组响应或观测值。
在定量研究中,收集完数据后,统计分析的第一步是描述这些响应的特征,例如一个变量(如年龄)的平均值,或两个变量(如年龄与创造力)之间的关系。
下一步是推断性统计,它帮助你判断数据是否支持或反驳你的假设,以及该结果是否可以推广到更大的总体。
描述性统计的类型
描述性统计主要有以下3种类型:
- 分布:关注每个数值出现的频率。
- 集中趋势:关注数值的平均情况。
- 变异性(离散程度):关注数值的分散程度。

你可以将这些方法应用于单个变量(单变量分析),也可以用于比较两个或多个变量(双变量或多变量分析)。
研究示例
你想研究不同休闲活动按性别划分的受欢迎程度。你发放了一份调查问卷,询问参与者在过去一年中每项活动进行了多少次:
- 去图书馆
- 在电影院看电影
- 参观国家公园
你的数据集就是这份调查的所有回答。现在,你可以使用描述性统计来了解每项活动的总体频率(分布)、每项活动的平均次数(集中趋势)以及每项活动回答的离散程度(变异性)。
频数分布
一个数据集由一系列数值(或分数)的分布组成。你可以通过表格或图表,以数字或百分比的形式,汇总某个变量所有可能取值的出现频次。这称为频数分布。
简单频数分布表 vs. 分组频数分布表
对于“性别”这一变量,你在左列列出所有可能的回答,然后在右列统计每种回答的数量或百分比。
| 性别 | 人数 |
|---|---|
| 男性 | 182 |
| 女性 | 235 |
| 其他 | 27 |
从这张表可以看出,参与本研究的女性人数多于男性或其他性别身份者。
集中趋势的度量
集中趋势的度量用于估计数据集的中心(或平均值)。均值、中位数和众数是三种常用的求平均的方法。
下面我们将用调查前6个回答为例,演示如何计算均值、中位数与众数。
均值(Mean)
均值(通常记为 M)是最常用的平均值计算方法。
要计算均值,只需将所有回答值相加,再除以回答总数。回答或观测的总数称为 N。
过去一年去图书馆的次数(均值)
- 数据集:15, 3, 12, 0, 24, 3
- 所有值之和:15 + 3 + 12 + 0 + 24 + 3 = 57
- 回答总数:N = 6
- 均值:57 ÷ 6 = 9.5
中位数(Median)
中位数是将数据从小到大排列后位于中间位置的数值。如果数据个数为偶数,则中位数是中间两个数的平均值。
过去一年去图书馆的次数(中位数)
- 排序后的数据集:0, 3, 3, 12, 15, 24
- 中间两个数:3 和 12
- 中位数:(3 + 12) ÷ 2 = 7.5
众数(Mode)
众数是数据集中出现频率最高的数值。
过去一年去图书馆的次数(众数)
- 数据集:0, 3, 3, 12, 15, 24
- 出现最多的数值:3(出现2次)
变异性的度量
变异性的度量让你了解回答值的分散程度。极差、标准差和方差分别反映了数据离散的不同方面。
极差(Range)
极差表示最极端的两个回答值之间的差距。计算方法是:最大值减去最小值。
过去一年去图书馆次数的极差
- 排序后的数据集:0, 3, 3, 12, 15, 24
- 极差:24 – 0 = 24
标准差(Standard Deviation)
标准差(记为 s 或 SD)表示数据集中各数值相对于均值的平均偏离程度。标准差越大,数据越分散。
计算标准差的六个步骤如下:
- 列出每个分数并计算其均值。
- 用每个分数减去均值得到偏差。
- 将每个偏差平方。
- 将所有平方偏差相加。
- 将平方偏差总和除以 N – 1。
- 对所得结果开平方根。
过去一年去图书馆次数的标准差
下表完成步骤1至4:
| 原始数据 | 与均值的偏差 | 偏差的平方 |
|---|---|---|
| 15 | 15 – 9.5 = 5.5 | 30.25 |
| 3 | 3 – 9.5 = -6.5 | 42.25 |
| 12 | 12 – 9.5 = 2.5 | 6.25 |
| 0 | 0 – 9.5 = -9.5 | 90.25 |
| 24 | 24 – 9.5 = 14.5 | 210.25 |
| 3 | 3 – 9.5 = -6.5 | 42.25 |
| 均值 M = 9.5 | 偏差总和 = 0 | 平方和 = 421.5 |
- 步骤5:421.5 ÷ 5 = 84.3
- 步骤6:√84.3 ≈ 9.18
由此可知,s = 9.18,即每个分数平均偏离均值约9.18次。
方差(Variance)
方差是偏差平方的平均值,反映数据集的离散程度。数据越分散,方差相对于均值就越大。
要计算方差,只需将标准差平方即可。方差的符号为 s²。
过去一年去图书馆次数的方差
- 数据集:15, 3, 12, 0, 24, 3
- s = 9.18
- s² = 84.3
单变量描述性统计
单变量描述性统计一次只关注一个变量。重要的是,应分别使用多种分布、集中趋势和离散程度的指标来检查每个变量的数据。SPSS 和 Excel 等软件可轻松计算这些指标。
去图书馆次数的单变量描述统计
| 指标 | 数值 |
|---|---|
| N(样本量) | 6 |
| 均值 | 9.5 |
| 中位数 | 7.5 |
| 众数 | 3 |
| 标准差 | 9.18 |
| 方差 | 84.3 |
| 极差 | 24 |
如果你仅考虑均值作为集中趋势的度量,异常值可能会扭曲你对数据“中心”的理解,而中位数或众数则不受此影响。
同样,虽然极差对异常值敏感,但你也应结合标准差和方差来获得更易比较的离散程度指标。
双变量描述性统计
如果你收集了多个变量的数据,可以使用双变量或多变量描述性统计来探索它们之间是否存在关系。
在双变量分析中,你同时研究两个变量的频数和变异性,以观察它们是否共同变化。你还可以在进行进一步统计检验之前,比较这两个变量的集中趋势。
多变量分析与双变量分析相同,只是涉及两个以上的变量。
列联表(Contingency Table)
在列联表中,每个单元格代表两个变量的交叉点。通常,自变量(如性别)放在纵轴,因变量(如活动)放在横轴。你可以“横向”阅读表格,以了解自变量与因变量之间的关系。
过去一年去图书馆的次数(原始数据)
| 群体 | 0–4 | 5–8 | 9–12 | 13–16 | 17+ |
|---|---|---|---|---|---|
| 儿童 | 32 | 68 | 37 | 23 | 22 |
| 成人 | 36 | 48 | 43 | 83 | 25 |
将原始数据转换为百分比后,列联表更易于解读。百分比使每一行具有可比性,仿佛每个群体都只有100名观察对象或参与者。创建基于百分比的列联表时,通常在每行末尾加上该自变量类别的总样本量(N)。
过去一年去图书馆的次数(百分比形式)
| 群体 | 0–4 | 5–8 | 9–12 | 13–16 | 17+ | N |
|---|---|---|---|---|---|---|
| 儿童 | 18% | 37% | 20% | 13% | 12% | 182 |
| 成人 | 15% | 20% | 18% | 35% | 11% | 235 |
从该表可以更清楚地看出:儿童和成人每年去图书馆超过17次的比例相近。此外,儿童最常去图书馆的次数区间是5–8次,而成人则是13–16次。
散点图(Scatter Plot)
散点图是一种展示两个或三个变量之间关系的图表,是变量间关系强度的可视化表示。
在散点图中,一个变量沿x轴绘制,另一个变量沿y轴绘制。每个数据点在图中以一个点表示。
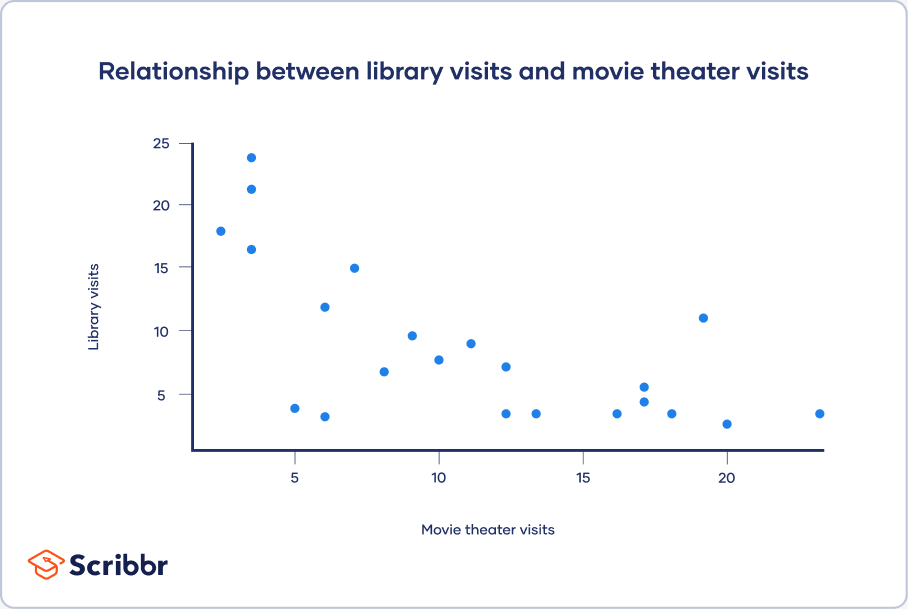
散点图示例:图书馆访问次数与电影院观影次数
你调查是否经常去图书馆的人较少去电影院看电影。你将参与者去电影院的次数绘制在x轴,去图书馆的次数绘制在y轴。
从散点图可以看出,随着去电影院次数的增加,去图书馆的次数减少。基于你对可能存在线性关系的视觉判断,你可以进一步进行相关性和回归分析。