从向量到张量：探索张量代数的数学原理

更新于 2026-02-06

Niklas Lang 2022-12-20

张量是线性代数中的一种数学函数，它将一组向量映射为一个数值。这一概念最初起源于物理学，随后被引入数学领域。或许最著名的使用张量概念的例子就是广义相对论。

在机器学习领域，张量被广泛用于多种应用的数据表示，例如图像或视频。它们构成了 TensorFlow 机器学习框架的基础，该框架的名称也正来源于此。

什么是秩（Rank）和轴（Axis）？

若要更精确地描述张量，我们需要引入所谓的“秩”（rank）和“维度”（dimension）。这些概念可用于确定张量对象的大小。为此，我们从一个矩阵出发，试图找出它的秩。我们可以先构建一个简单的 NumPy 数组，用以表示一个具有三行三列的矩阵。

import numpy as np 

matrix = np.array([
                   [1,5,7],
                   [2,9,4],
                   [4,4,3]
                  ])

张量的“秩”提供了关于引用其中单个数值所需索引数量的信息。它也常被称为“维度数”。

以矩阵为例，这意味着它具有秩 2（即二维），因为我们需要两个索引来输出一个特定的数值。假设我们希望从“矩阵”这个对象中获取位于第一行第二列的数字 5，那么我们需要两个步骤才能到达该位置。

首先，必须通过索引 0 引用第一行：

matrix[0]

array([1, 5, 7])

在所得到的数组中，我们可以通过索引 1 选择第二个元素（注意：在 NumPy 中，索引从 0 开始！）：

matrix[0][1]  # 或 matrix[0, 1]

5

因此，矩阵具有秩 2（是二维的），因为需要两个索引才能获取一个数值。然而，矩阵有许多不同的尺寸，例如三行四列、五行两列等。

为了区分不同的矩阵并对其进行精确定义，我们使用所谓的“轴”（axis）及其长度。“轴”指的是张量在某一特定维度中的值。以我们的“矩阵”为例，NumPy 数组中第一个索引对应的是第一维的一个轴。

# First axis of the first dimension of the object "matrix"
print(matrix[0])

[1 5 7]

轴的长度则说明了沿该轴存在多少个有效索引。在我们的例子中，第一轴的长度为 3，因为该轴上总共有三个索引（即矩阵有三行）。以下调用会导致错误，因为第四个索引并不存在：

# Returns an error since there is no fourth index in "matrix"
matrix[3] 

IndexError: index 3 is out of bounds for axis 0 with size 3

张量的尺寸（Size）是什么？

张量的尺寸给出了每个维度上各轴的长度。这意味着我们可以如下方式指定“矩阵”对象的尺寸：

import tensorflow as tf

matrix = tf.convert_to_tensor(matrix)
tf.shape(matrix)

在 TensorFlow 中，我们会收到各种反馈信息，这些信息相对容易理解。该张量具有“Shape”为 2，即秩为 2 或两个维度。这一点我们早已预料到，因为我们知道矩阵是一个二维张量。“dtype”描述了所存储的数据类型，在本例中为整数。最后，我们通过“([3,3])”得到了张量的尺寸，因为在两个维度中，每个维度都有三个不同的索引。这一结果也符合预期，因为这是一个三行三列的矩阵。

张量有哪些不同类型？

张量是向量和矩阵的统称，在机器学习领域中泛指多维数组。根据数组的维度不同，可区分为以下几种类型：

标量（Scalar）

标量，即单个数字，是一个 0 维张量。不需要任何索引即可引用该数值。因此，标量没有轴，其秩为 0。

向量（Vector）

向量是一维张量，秩为 1。向量包含的元素数量决定了其轴的长度。

矩阵（Matrix）

正如我们前面详细描述的那样，矩阵是一个二维张量。

张量（Tensor）

从三维或更高维度开始，通常就直接称为张量。一个三维张量可以被想象为多个矩阵的集合。

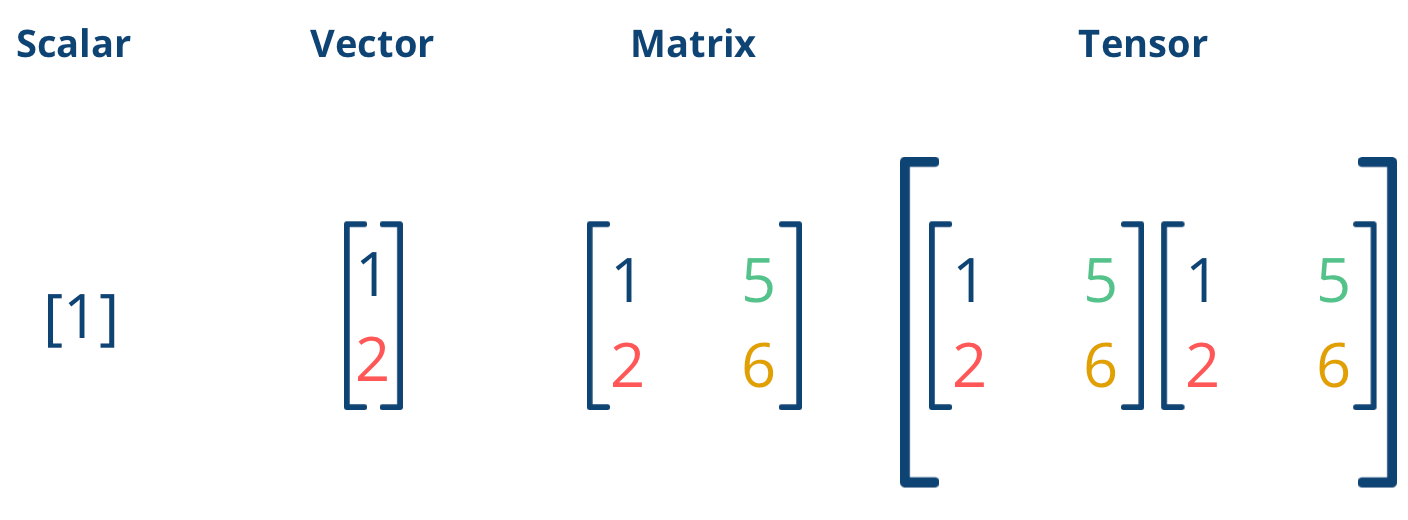img 不同对象在 Python 编程中的表示 | 来源：作者

张量是对线性代数中已有对象的推广。它们在编程中被广泛使用，主要是因为能够表示多维数据结构。

可以对张量执行哪些算术运算？

张量允许的算术运算与矩阵非常相似，但在命名上可能略有不同：

  • 加法：如果两个对象具有相同的维度，它们可以通过逐元素相加的方式进行加法运算，并生成一个具有相同维度的新对象。
  • 减法：如果两个对象具有相同的维度，它们可以通过逐元素相减的方式进行减法运算，并生成一个具有相同维度的新对象。
  • 哈达玛积（Hadamard Product）：这种特殊的乘积通过逐元素相乘得到。之所以使用特殊名称，是因为还存在基于矩阵乘法的“常规”乘法方式。
  • 除法：如果两个对象具有相同的维度，它们可以通过逐元素相除的方式进行除法运算，并生成一个具有相同维度的新对象。

张量在机器学习中的作用是什么？

为了训练机器学习模型，需要大量数据。然而，现实世界中的原始数据并非以模型可以直接使用的数学形式存在。因此，我们必须先将图像、视频或文本等数据转换为多维数据结构，以便进行数学处理。

同时，由于神经网络自身的结构特性，它们能够容纳并输出远超传统向量和矩阵的多种维度。因此，随着神经网络的普及，张量的使用也变得更加普遍。

以下应用在机器学习中利用张量来提升模型性能：

协同过滤（Collaborative Filtering）

该模型常用于电子商务领域，例如根据用户以往的购买行为，在网站上为其推荐最合适的产品。在训练过程中，传统方法使用一个矩阵，其中行代表用户，列代表产品。如果第一行的用户曾购买过第二列的产品，则在该位置标记为 1，否则标记为 0。尽管这种设置已能取得良好效果，但通过在矩阵中增加额外维度（例如包含用户上下文信息），进一步提升了推荐效果。

计算机视觉（Computer Vision）

图像和视频无法仅用纯矩阵表示。它们不仅包含大量像素，而且是通过叠加不同颜色而形成的。以简单的 RGB 格式图像为例，图像是由红（Red）、绿（Green）、蓝（Blue）三种颜色通道叠加而成。

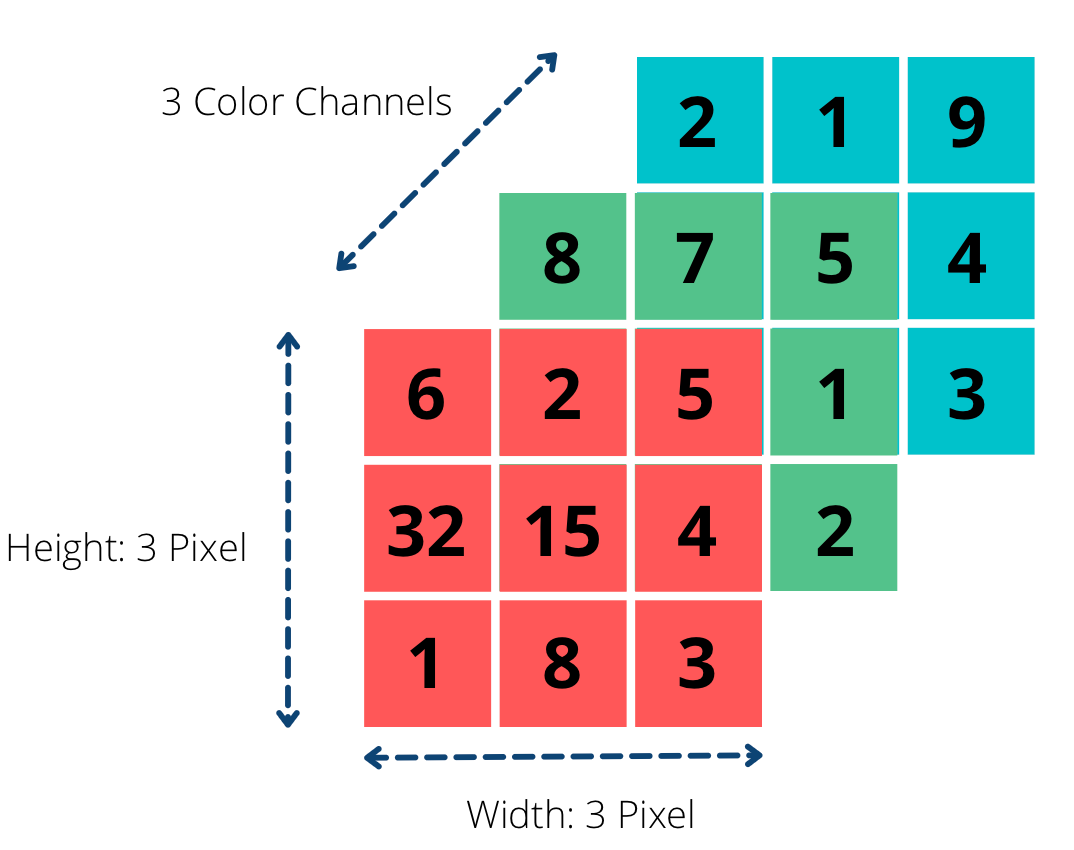img 图像的张量表示 | 来源：作者

张量分析中会出现哪些问题？

张量是多维数组，在物理学、工程学和机器学习等多个科学领域中都具有基础性地位。尽管张量为表示复杂数据提供了强大工具，但其分析过程仍面临诸多挑战。以下是张量分析中的一些主要难题：

  1. 高维性（High dimensionality）：张量可能具有许多维度，随着维度数量的增加，数据分析和可视化变得愈发困难。
  2. 稀疏性（Sparse data）：张量可能非常稀疏，即大多数条目为零。这使得传统的线性代数技术难以有效应用于分析。
  3. 非唯一性（Non-uniqueness）：张量可能存在多个在数学上等价的不同表示形式，这使得难以确定数据背后的真实结构。
  4. 计算复杂度（Computational complexity）：分析大型张量在计算上可能非常昂贵且耗时。
  5. 数据预处理（Data preprocessing）：构建张量所需的数据预处理过程本身具有挑战性，尤其是在处理高维、稀疏或含噪声的数据时。
  6. 结果解释（Interpretation）：解释张量分析的结果可能十分困难，尤其是在处理复杂、多维数据时。

尽管存在上述挑战，张量分析和机器学习技术的进步正使我们越来越能够从高维数据中提取有意义的洞察。未来，我们可以期待张量分析领域的进一步发展，从而充分释放这一强大数据表示技术的全部潜力。

你应该记住的关键点

  • 张量是来自线性代数的数学对象，用于表示多维对象。
  • 它们可以执行与向量或矩阵类似的算术运算。
  • 在机器学习中，张量被用于实现更优的推荐系统，或将图像和视频映射为数据结构。