Python 集合（Set）深度指南

更新于 2026-01-13

Juliano Luiz Faccioni 2023-09-04

通过本指南深入掌握 Python 集合。你将全面了解集合操作、常用方法，并学习这一基础数据结构的实际应用场景。

你听说过 Python 的集合（set）吗？虽然它不像列表（list）和字典（dict）那样广为人知，但忽视集合是一个错误：它与列表一样灵活，可用于构建复杂的过滤逻辑，并且在许多场景下性能远超其他数据类型。

在本篇 Python 集合指南中，我们将首先定义什么是集合；接着详细介绍 Python 中的集合操作及可用方法；最后展示如何在实际场景中有效利用集合。

什么是 Python 集合？

简而言之，Python 集合是一种可变的、无序的、由唯一不可变元素组成的容器。让我们逐项解释这些特性：

  • 可变（Mutable）：集合的大小不固定，你可以向其中添加或删除元素。
  • 容器（Collection）：你可以使用 for 循环遍历集合中的元素。
  • 无序（Unordered）：你无法获取“第一个”或“最后一个”元素，也无法保证遍历时元素的顺序。可以把集合想象成一个装满物品的袋子：你可以往里加东西或拿走东西，但问“袋子里第一个是什么”是没有意义的。
  • 元素唯一（Unique Elements）：集合中不能包含重复值。即使你多次添加相同的元素，集合也只会保留一份。
  • 元素必须不可变（Immutable Elements）：虽然集合本身是可变的，但其内部元素必须是不可变类型。因此，像列表（list）和字典（dict）这样的可变对象不能作为集合的元素。

乍看之下，Python 集合似乎并不惊艳。但它最强大的能力之一，正是通过集合运算来高效地组合和筛选多个集合中的元素。

Python 中的集合运算

Python 集合最突出的优势在于其内置的集合运算。这些运算能以多种方式快速合并或筛选多个集合中的元素，而且执行速度极快——远胜于通过循环手动处理列表等结构。

为便于理解，我们先定义两个集合：

A = {1, 2, 4, 6, 8}
B = {1, 2, 3, 4, 5}

注意：定义集合时使用花括号 {} 包裹元素，并用逗号分隔。

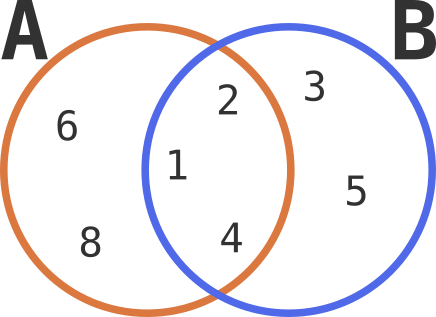
image

下面我们将逐一介绍核心的集合运算。

并集（Union）

并集将所有集合中的元素合并在一起，自动去重。在 Python 中，可通过 .union() 方法或 |（管道符）实现：

A = {1, 2, 4, 6, 8}
B = {1, 2, 3, 4, 5}

# 使用 .union() 方法
print(A.union(B))

# 使用 | 运算符
print(A | B)

# 输出：
# {1, 2, 3, 4, 5, 6, 8}

注意结果中没有重复元素。

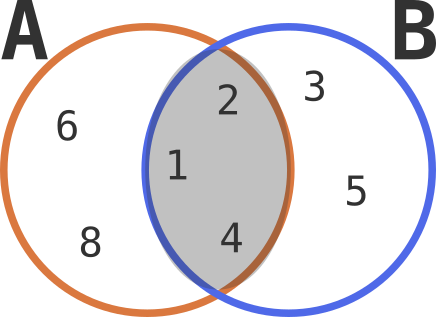
image

交集（Intersection）

交集返回两个集合中共同存在的元素。可通过 .intersection() 方法或 &（按位与）运算符实现：

A = {1, 2, 4, 6, 8}
B = {1, 2, 3, 4, 5}

# 使用方法
print(A.intersection(B))

# 使用 & 运算符
print(A & B)

# 输出：
# {1, 2, 4}

只有同时出现在 A 和 B 中的元素才会被保留。

image

差集（Difference）

A 对 B 的差集表示“在 A 中但不在 B 中”的元素。可通过 .difference() 方法或 -（减号）运算符实现：

A = {1, 2, 4, 6, 8}
B = {1, 2, 3, 4, 5}

# A - B
print(A.difference(B))  # 或 A - B
# 输出：{6, 8}

⚠️ 注意：差集运算顺序敏感！A - B 与 B - A 结果不同：

print(B - A)  # 输出：{3, 5}

image

对称差集（Symmetric Difference）

对称差集返回只存在于其中一个集合中的元素（即排除交集部分）。使用 .symmetric_difference() 方法：

A = {1, 2, 4, 6, 8}
B = {1, 2, 3, 4, 5}

print(A.symmetric_difference(B))
# 输出：{3, 5, 6, 8}

这相当于 (A - B) ∪ (B - A)，也可以理解为“并集中去掉交集”。

image

超集、子集与成员检测

除了上述运算，Python 集合还提供判断集合间包含关系的方法。

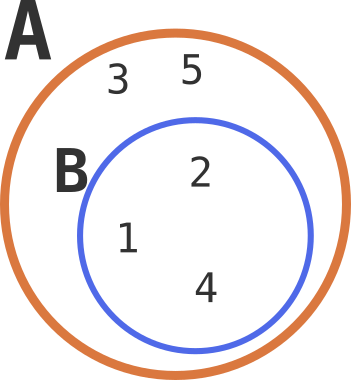
超集与子集

考虑以下两个集合：

A = {1, 2, 3, 4, 5}
B = {1, 2, 4}
  • 因为 B 的所有元素都在 A 中，所以 A 是 B 的超集（superset），B 是 A 的子集（subset）。

使用 .issuperset() 和 .issubset() 判断：

print(A.issuperset(B))  # True
print(B.issubset(A))    # True

image

💡 补充知识：

  • 空集是任何集合的子集。
  • 任何集合都是自身的子集和超集。

成员检测

使用 in 关键字检查元素是否在集合中：

B = {1, 2, 4}
print(1 in B)  # True
print(3 in B)  # False

集合的成员检测平均时间复杂度为 O(1)，比列表快得多！

创建与操作集合

创建集合

  1. 字面量语法（推荐）：

    S = {1, 10, 100}

  2. 使用 set() 构造函数（适用于从其他序列转换）：

    S = set([1, 10, 100])

  3. 创建空集合（⚠️不能用 {}，那会创建空字典！）：

    empty_set = set()

修改集合

  • 添加元素：.add()

    S = set()
S.add(2)  # {2}
S.add(2)  # 无变化（去重）

  • 删除元素：.remove()（若元素不存在会抛出 KeyError）

    S.remove(2)  # 删除后 S 为空

  • 批量添加：.update()

    A = {1, 2, 3}
B = {3, 4, 5}
S = set()
S.update(A)  # {1, 2, 3}
S.update(B)  # {1, 2, 3, 4, 5}

  • 复制与清空：

    S1 = {1, 2, 3}
S2 = S1.copy()  # 独立副本
S1.clear()      # S1 变为空集

遍历集合

S = {1, 2, 3, 4, 5}
for number in S:
    print(number)

⚠️ 重要提醒：遍历顺序是不确定的！即使有时看起来有序，Python 也不保证顺序。如需有序，请使用列表。

Python 集合的典型应用场景

尽管集合看似小众，但在实际开发中用途广泛。

场景 1：列表去重

将列表转为集合再转回列表，即可快速去重：

values = [1, 2, 2, 1, 3, 4, 1, 2, 3, 4, 1]
unique_values = list(set(values))
print(unique_values)  # [1, 2, 3, 4]（顺序不定）

✅ 优点：简洁高效
⚠️ 缺点：会丢失原始顺序（如需保留顺序，可使用 dict.fromkeys()）

场景 2：数据过滤与分析

假设你有三组客户 ID：

all_clients = {104, 203, 255, 289, 448}
clients_bought_X = {104, 448}
clients_bought_Y = {104, 255, 289}

你可以轻松回答以下问题：

Q1：买了 X 但没买 Y 的客户？

print(clients_bought_X - clients_bought_Y)  # {448}

Q2：同时买了 X 和 Y 的客户？

print(clients_bought_X & clients_bought_Y)  # {104}

Q3：什么都没买的客户？

purchasers = clients_bought_X | clients_bought_Y
print(all_clients - purchasers)  # {203}

💡 当数据量达到数千甚至数万时，集合运算的性能优势将极为显著！

总结

Python 集合虽低调，却是处理唯一性、成员关系和集合逻辑的利器。掌握以下要点：

  • 集合 = 无序 + 唯一 + 元素不可变
  • 核心运算：|（并）、&（交）、-（差）、^（对称差）
  • 实用方法：.add(), .remove(), .issubset(), .issuperset()
  • 典型应用：去重、成员检测、数据过滤

现在就去尝试用集合解决你的下一个编程问题吧！