Log-loss得分背后的直觉

Gaurav Dembla 2020-11-17

在机器学习中，分类问题指的是需要为给定的观察（记录）预测一个类别标签的预测建模。虽然输入数据（特征）可以由连续变量或分类变量组成，但输出始终是一个分类变量。例如，基于诸如湿度、温度、“多云/晴朗”、风速等天气信息以及一年中的时间来预测今天你的城市是否会“下雨”。另一个例子是，根据电子邮件的内容和发件人信息，预测它是“垃圾邮件”还是“非垃圾邮件”。

Log-loss是评估分类问题性能的主要指标之一。但它概念上意味着什么呢？当你在网上搜索这个术语时，很容易找到直接深入探讨所涉及数学的好文章和博客。话虽这么说，我计划在这里采取不同的方法——先谈谈该指标背后的直觉，然后再提供用于计算该指标的公式。

记住，还有另一个重要指标被广泛用于评估分类算法的性能——ROC-AUC得分。一旦你对log-loss得分有了深刻的理解，你可能想要阅读我的另一篇博客《ROC-AUC得分背后的直觉》，特别是对比这两个指标。

这篇博客力求回答以下问题：

什么是预测概率？
Log-loss概念上意味着什么？
如何计算Log-loss值？
模型的Log-loss得分如何计算？
如何解释Log-loss得分？

什么是预测概率？

二分类算法首先预测一条记录被归类到类别1的概率，然后根据该概率是否超过阈值（通常默认设置为0.5）将数据点（记录）分类到两个类别（1或0）之一。

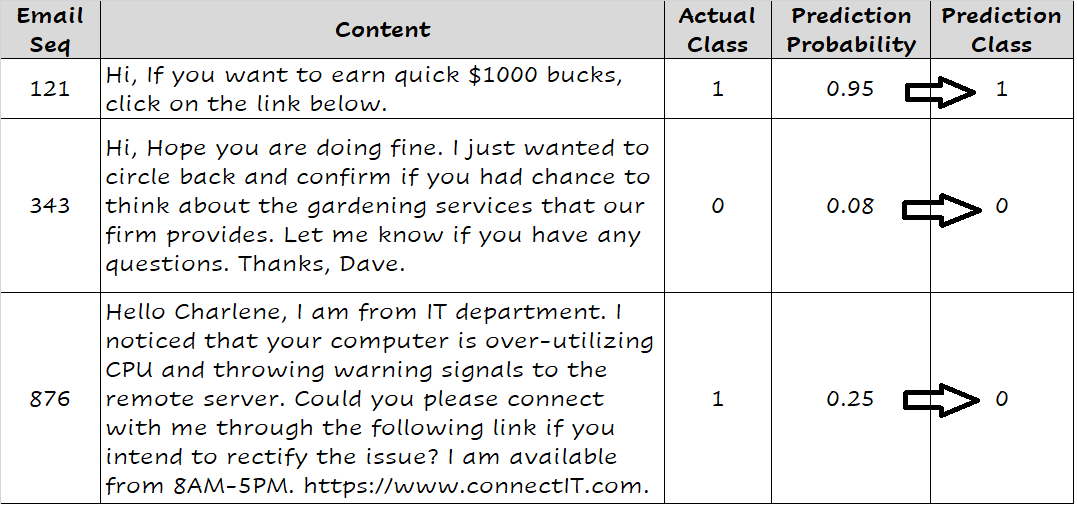
因此，在预测记录的类别之前，模型必须预测该记录被分类到类别1的概率。请记住，正是这种数据记录的预测概率决定了log-loss值。

Log-loss概念上意味着什么？

Log-loss表明预测概率与对应的真值（在二分类情况下为0或1）之间的接近程度。预测概率偏离实际值越大，log-loss值越高。

考虑垃圾邮件与非垃圾邮件分类的问题。让我们用1表示垃圾邮件类别，用0表示非垃圾邮件类别。考虑一封垃圾邮件（实际值=1），并且一个统计模型预测这封邮件为垃圾邮件的概率为1。由于预测概率完全没有偏离实际值1，因此与该预测相关的log-loss值为0，表示完全没有误差。（实际上，log-loss值足够小以至于可以认为是0）。我们将在建立了对该术语的概念理解后讨论其计算方法。

考虑另一封垃圾邮件，其预测概率为0.9。模型的预测概率比实际值1低了0.1，因此，该预测的log-loss值大于零（精确地说，是0.105）。

现在，让我们看一封非垃圾邮件。模型预测它成为垃圾邮件的概率为0.2，换句话说，假设默认的概率阈值为0.5，模型会将其分类为非垃圾邮件。预测概率与实际值0（因为它是非垃圾邮件）之间的绝对差是0.2，这比我们在前两个观察中看到的要大。与该预测相关的log-loss值为0.223。

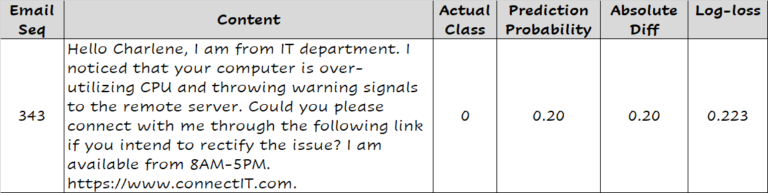
注意，较差的预测（离实际值更远）的log-loss值高于较好的预测（接近实际值）的log-loss值。

现在，假设有一组5封不同的垃圾邮件，它们的预测概率范围很广（成为垃圾邮件的概率）——1.0、0.7、0.3、0.009和0.0001。你现在可能在想，一封垃圾邮件怎么可能被预测成垃圾邮件的概率仅为0.0001。让我们继续这个假设，并且假定训练的统计模型并不是完美的，因此在最后三个观测上做得非常糟糕（可能会将其分类为非垃圾邮件，因为它们的预测概率更接近于0而不是1）。请注意，随着观测的预测远离实际值1，log-loss值似乎以指数而非线性的方式增加。

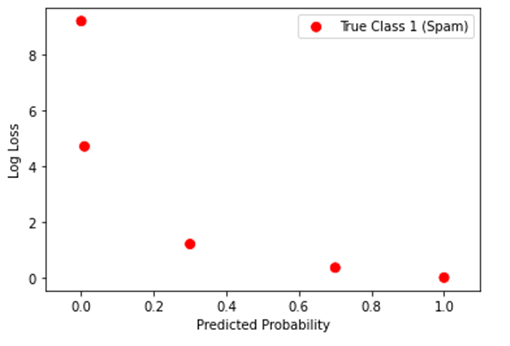
事实上，如果我们使用所有可能的预测概率（从0到1）来预测垃圾邮件，图表如下所示。对于真实的1观测，预测概率越低，其log-loss值就越高。

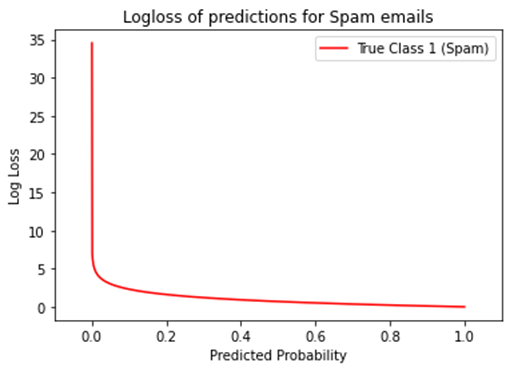
同样地，对于一系列不同概率预测的非垃圾邮件，图表如下所示，是上述图的镜像。对于真实的0观测，预测概率越高，其log-loss值就越高。

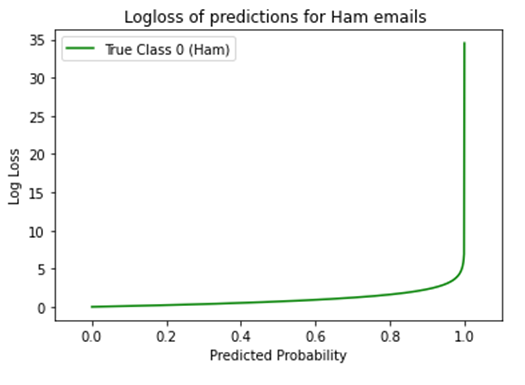
总之，预测概率距离实际值越远，其log-loss值就越高。

在训练分类模型时，我们希望尽可能准确地预测每个观测的概率，使其接近实际值（0或1）。因此，log-loss成为一个训练和优化分类模型的良好选择，其中预测概率与其真实值的距离越大，预测受到的惩罚就越重。

如何计算Log-loss值？

既然你了解了log-loss背后的直觉，我们可以讨论公式及其计算方法。

$\text{Logloss}_i = -[y_i \ln(p_i) + (1-y_i) \ln(1-p_i)]$

其中 $i$ 是给定的观察/记录， $y$ 实际/真值， $p$ 是预测概率， $\ln$ 指数字的自然对数（以 $e$ 为底的对数值）。

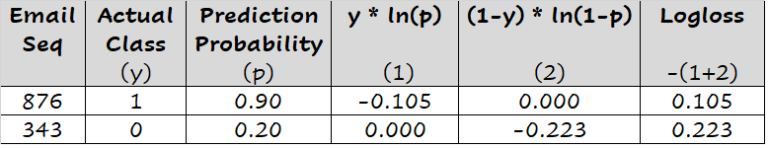
模型的Log-loss得分如何计算？

如上所示，log-loss值根据观察的实际值（ $y$ ）和预测概率（ $p$ ）计算。为了评估模型并总结其技能，分类模型的log-loss得分报告为所有观察/预测的log-loss值的平均值。如下所示，给定三个预测的log-loss值的平均值为0.110。

$\text{Logloss} = \frac{1}{N}\sum_{i=1}^{N}logloss_i$

$\text{Logloss} = -\frac{1}{N}\sum_{i=1}^{N}[y_i \ln(p_i) + (1-y_i) \ln(1-p_i)]$

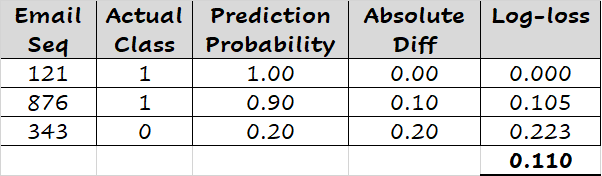
其中 $N$ 是观察的数量（此处为3）。

完美技能的模型的log-loss得分为0。换句话说，该模型预测每个观测的概率等于实际值。

对于分类问题而言，log-loss得分相当于回归问题中的均方误差（MSE）。这两个指标都表明预测结果有多好或多坏，通过指出预测值与实际值之间的差距。

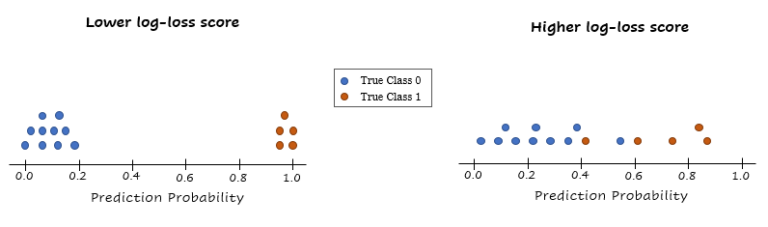
具有较低log-loss得分的模型优于具有较高log-loss得分的模型，前提是这两个模型应用于相同分布的数据集。我们不能比较应用于两个不同数据集的两个模型的log-loss得分。

如何解释Log-loss得分？

考虑一组10封电子邮件的例子，其中有9封是非垃圾邮件。由于只有1封邮件（共10封）是垃圾邮件，我们可以构建一个简单的分类模型，简单地预测每封邮件成为垃圾邮件的概率为0.1。如下所示，此简单模型的log-loss得分为0.325。

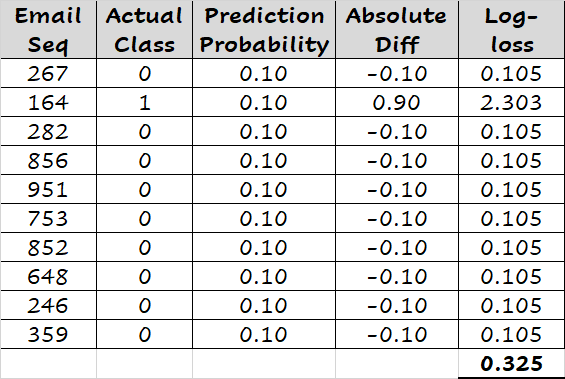
如下所示，将每封邮件的预测概率重置为0.08（略小于0.1），log-loss得分变为0.328。同样，如果我们将预测概率设置为0.12（略大于0.1），我们得到的log-loss得分为0.327。简而言之，如果我们将邮件的预测概率设置为任何其他值而不是0.1，我们会得到更高的log-loss得分。

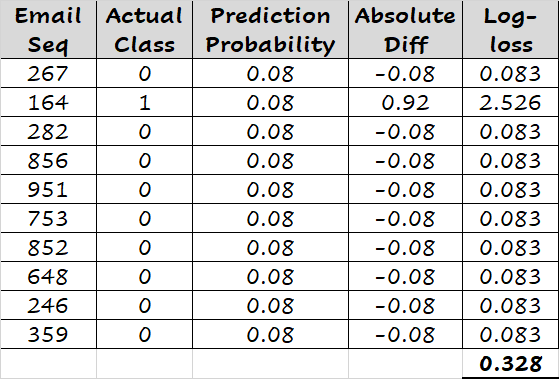
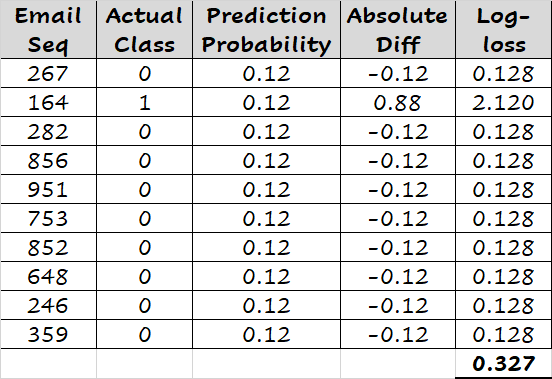
下图也证实了我们的发现——将邮件的概率设置为0.1会产生最低的log-loss得分，这将是给定样本数据集的基准分数。

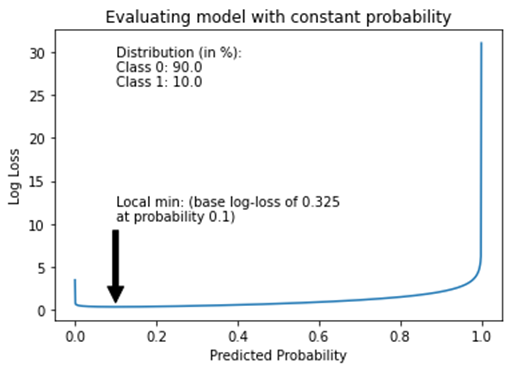
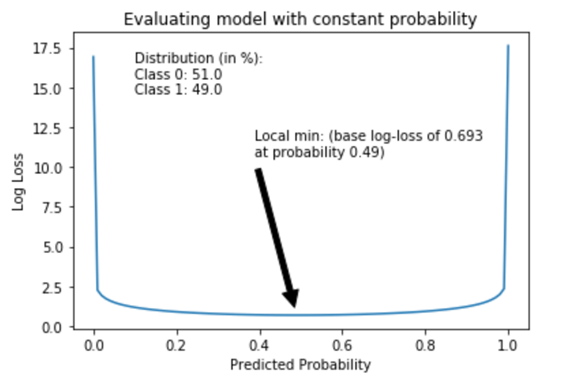
数据集的基准log-loss得分是由简单分类模型确定的，该模型简单地将所有观察赋予一个等于%数据类别1观察值的常量概率。对于平衡的数据集，类别0与类别1的比例为51:49，具有常量概率0.49的简单模型将产生log-loss得分为0.693，这被视为该数据集的基准分数。

数据集中不平衡程度越高，数据集的基准log-loss得分越低，由于影响log-loss值平均值的观察比例（在此情况下，类别1）较低。

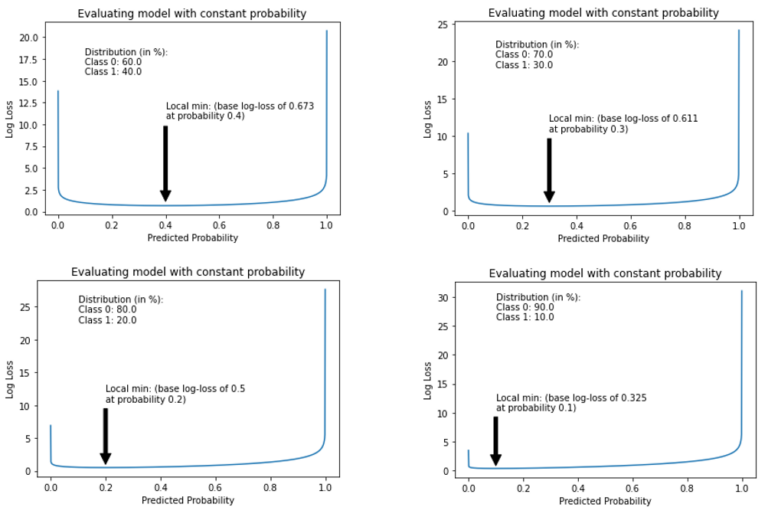
由于预测不平衡数据集的一个低恒定概率值会导致非常低的log-loss值，因此在这种情况下，使用log-loss评估模型技能应谨慎解读。实际上，log-loss值应始终结合由简单模型提供的基准分数来解释。

当我们基于给定数据集构建一个统计模型时，该模型必须击败基准log-loss得分，从而证明自己比简单模型更有技巧。如果没有达到这一点，则意味着训练的统计模型根本没有帮助，最好直接采用简单模型。