使用 scikit-learn 进行 K-近邻（KNN）分类

Adam Shafi 2023-02-20

本文介绍了如何以及何时使用 scikit-learn 实现 k-近邻（k-Nearest Neighbors, kNN）分类。内容聚焦于核心概念、工作流程和实际示例。我们还将讨论距离度量方法，以及如何通过交叉验证选择最优的 k 值。

本教程将涵盖 k-近邻（kNN）算法的概念、工作流程和示例。kNN 是一种流行的监督学习模型，既可用于分类也可用于回归，是理解距离函数、投票机制和超参数优化的绝佳方式。

要从本教程中获得最大收益，你应该具备 Python 的基础知识，并有使用 DataFrame 的经验。如果你熟悉 scikit-learn 的基本语法会更有帮助。需要注意的是，kNN 经常与无监督方法 k-Means 聚类混淆。如果你对此感兴趣，可以阅读《使用 scikit-learn 在 Python 中实现 k-Means 聚类》。你也可以立即注册我们的 Python 机器学习课程，该课程对 kNN 有更深入的讲解。

虽然 kNN 可用于分类和回归，但本文将专注于构建分类模型。在机器学习中，分类是一种监督学习任务，其目标是为给定的输入数据点预测一个类别标签。该算法在带标签的数据集上进行训练，利用输入特征学习输入与对应类别标签之间的映射关系。训练完成后，我们可以使用该模型对新的、未见过的数据进行预测。

K-近邻算法概述

kNN 算法可以被看作一种“投票系统”：对于一个新的数据点，算法会查看其在特征空间中最近的 k 个邻居（k 为整数），然后根据这 k 个邻居中占多数的类别标签来决定该新数据点的类别。想象一个只有几百名居民的小村庄，你需要决定自己应该支持哪个政党。你可能会去问离你最近的邻居们各自支持哪个政党。如果在你的 k 个最近邻居中，大多数人都支持 A 党，那么你很可能也会投票给 A 党。这与 kNN 算法的工作原理非常相似：新数据点的类别由其 k 个最近邻居中的多数类别决定。

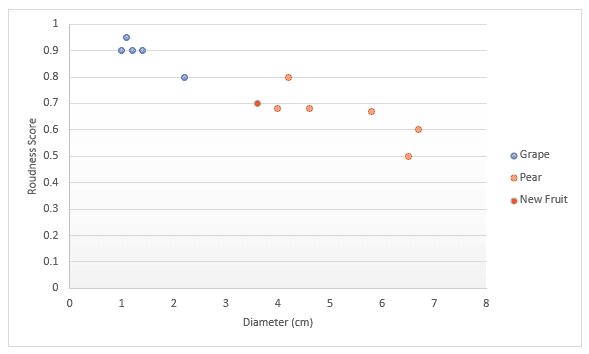
让我们通过另一个例子更深入地理解。假设你有关于水果的数据，具体是葡萄和梨。你有一个衡量水果“圆度”的分数，以及水果的直径。你可以将这两个特征绘制在一张图上。当有人给你一个新水果时，你可以将其也画在这张图上，然后测量它到 k 个最近数据点的距离，从而判断它属于哪种水果。如下图所示：如果我们选择 k=3，那么三个最近的点都是梨，因此我们可以 100% 确定这是一个梨；如果我们选择 k=4，其中三个是梨，一个是葡萄，那么我们会说有 75% 的把握认为这是一个梨。我们将在本文后面部分详细讨论如何选择最佳的 k 值，以及不同的距离度量方法。

数据集

为了进一步说明 kNN 算法，我们来看一个数据科学家在工作中可能遇到的案例研究。假设你是一家在线零售商的数据科学家，任务是检测欺诈交易。目前你仅有的两个特征是：

dist_from_home：用户家庭位置与交易发生地点之间的距离。
purchase_price_ratio：本次交易商品价格与该用户历史购买商品价格中位数的比值。

该数据包含 39 条观测记录，每条记录代表一笔交易。在本教程中，数据已存储在变量 df 中，其形式如下：

	dist_from_home	purchase_price_ratio	fraud
0	2.1	6.4	1
1	3.8	2.2	1
2	15.7	4.4	1
3	26.7	4.6	1
4	10.7	4.9	1

其中 fraud 列表示是否为欺诈交易（1 表示欺诈，0 表示正常）。

K-近邻工作流程

我们将遵循《机器学习工作流程》信息图来拟合并训练该模型。

机器学习工作流程信息图来源

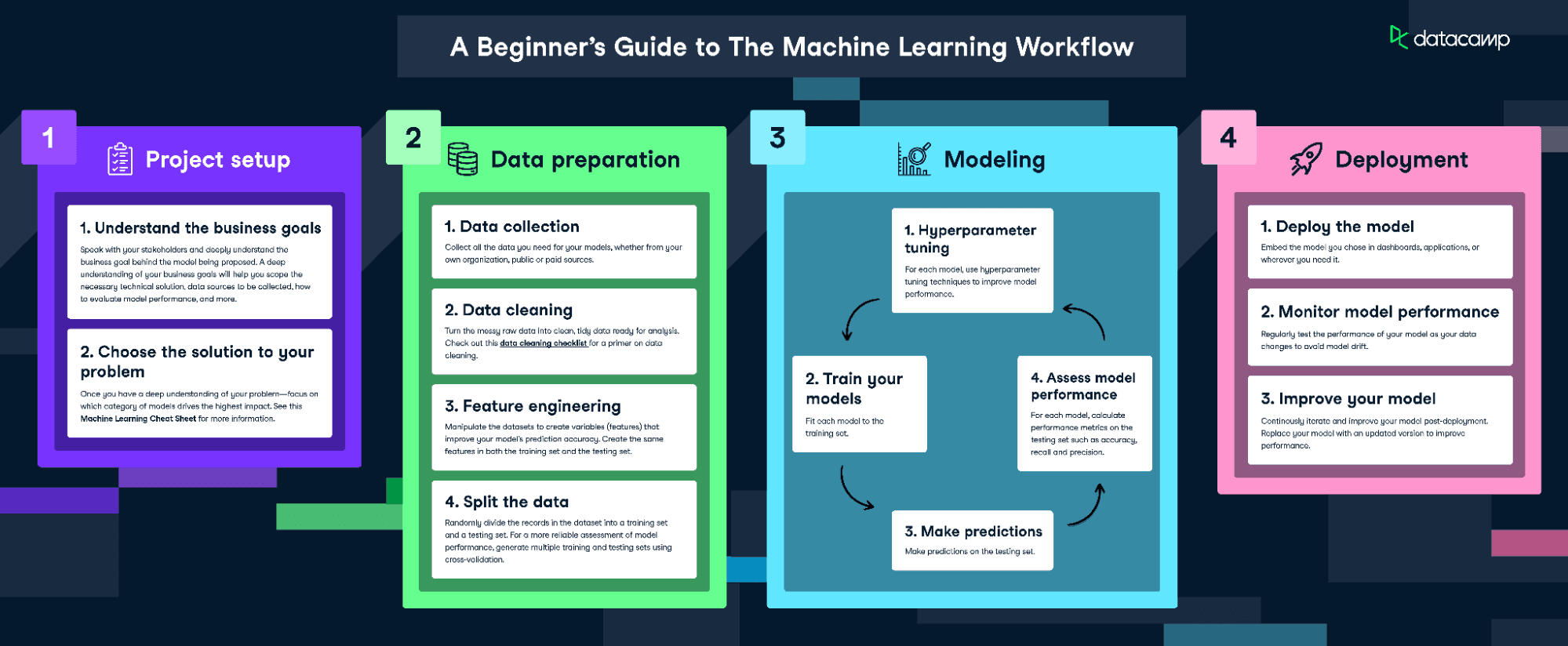
不过，由于我们的数据相当干净，不会执行所有步骤。我们将完成以下环节：

特征工程
数据划分
模型训练
超参数调优
模型性能评估

可视化数据

首先，我们使用 Matplotlib 对数据进行可视化，将两个特征绘制为散点图：

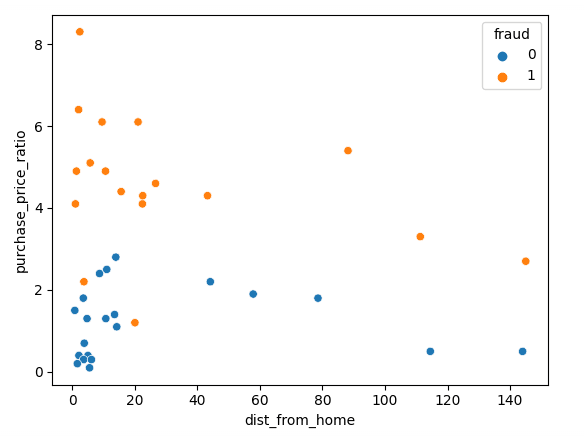
sns.scatterplot(x=df['dist_from_home'], y=df['purchase_price_ratio'], hue=df['fraud'])

如图所示，欺诈交易与正常交易之间存在明显差异：欺诈交易的商品价格比用户历史中位数高得多。而关于“距家距离”的趋势则较难解释——正常交易通常更靠近家，但也存在若干异常值。

数据标准化与划分

在训练任何机器学习模型时，将数据划分为训练集和测试集非常重要。训练集用于拟合模型，算法通过训练集学习特征与目标之间的关系，并尝试从中发现可用于预测新数据的模式。测试集用于评估模型性能：模型对测试集进行预测，并将预测结果与真实标签进行比较。

在训练 kNN 分类器时，必须对特征进行标准化。这是因为 kNN 依赖于点与点之间的距离计算。默认使用的是欧几里得距离（Euclidean Distance），即两点间各维度差值平方和的平方根。在我们的数据中，purchase_price_ratio 的取值范围约为 0 到 8，而 dist_from_home 的数值要大得多。如果不进行标准化，距离计算将严重偏向 dist_from_home，因为它的数值更大。

标准化应在划分训练/测试集之后进行，以防止“数据泄露”（data leakage）——如果先对全部数据标准化，再划分，那么标准化过程会无意中将测试集的信息泄露给训练过程。

以下代码首先将数据划分为训练集和测试集，然后使用 scikit-learn 的 StandardScaler 进行标准化。我们先对训练集调用 .fit_transform()，使缩放器学习训练集的均值和标准差；然后对测试集调用 .transform()，使用之前学到的参数进行变换。

# 将数据划分为特征 (X) 和目标 (y)
X = df.drop('fraud', axis=1)
y = df['fraud']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 使用 StandardScaler 对特征进行标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

拟合与评估模型

现在可以训练模型了。我们先固定 k=3（后续会优化该值）。首先创建 kNN 模型实例，然后用训练数据进行拟合。我们将特征和目标变量同时传入，以便模型学习它们之间的关系。

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

模型现已训练完成！我们可以对测试集进行预测，用于后续评分。

y_pred = knn.predict(X_test)

评估模型最简单的方式是使用准确率（accuracy）：将预测结果与测试集中的真实标签进行比较，统计模型预测正确的比例。

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

输出：

Accuracy: 0.875

这个分数相当不错！但我们或许可以通过优化 k 值获得更好的性能。

使用交叉验证选择最优 k 值

遗憾的是，没有神奇的方法可以直接确定最佳 k 值。我们必须遍历多个 k 值，然后根据结果做出判断。

在下面的代码中，我们设定 k 的取值范围为 1 到 30，并创建一个空列表用于存储结果。我们使用交叉验证（cross-validation）来计算每个 k 值对应的准确率。这意味着我们无需手动划分训练/测试集（但仍然需要标准化数据）。我们遍历每个 k 值，使用 cross_val_score 计算其交叉验证得分，并将平均分存入列表。

具体来说，我们使用 scikit-learn 的 cross_val_score 函数。传入 kNN 模型实例、数据以及折数（cv=5）。这意味着模型会将数据分成 5 个等大小的组，每次用其中 4 组训练、1 组测试，循环 5 次，最终返回 5 个准确率分数，我们取其平均值作为该 k 值的性能指标。

k_values = [i for i in range(1, 31)]
scores = []

scaler = StandardScaler()
X = scaler.fit_transform(X)

for k in k_values:
    knn = KNeighborsClassifier(n_neighbors=k)
    score = cross_val_score(knn, X, y, cv=5)
    scores.append(np.mean(score))

我们可以用以下代码绘制结果：

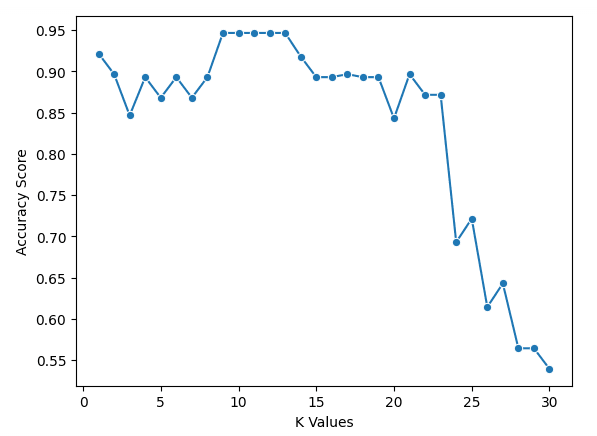
sns.lineplot(x=k_values, y=scores, marker='o')
plt.xlabel("K Values")
plt.ylabel("Accuracy Score")

从图表可以看出，k = 9、10、11、12 和 13 时，准确率均略低于 95%。由于这些 k 值性能相当，建议选择较小的 k 值。这是因为较大的 k 值会引入更多远离目标点的邻居，可能引入噪声。当然，你也可以探索其他评估指标。