损失函数及其在神经网络中的应用

Vishal Yathish 2022-08-04

损失函数是神经网络中最重要的组成部分之一，因为它们（连同优化函数）直接负责将模型拟合到给定的训练数据上。

本文将深入探讨损失函数在神经网络中的使用方式、不同类型的损失函数、如何在 TensorFlow 中编写自定义损失函数，以及损失函数在处理图像和视频训练数据方面的实际实现——这些正是我所关注和聚焦的计算机视觉领域的主要数据类型。

背景知识

首先，快速回顾一下神经网络的基本原理及其工作方式。

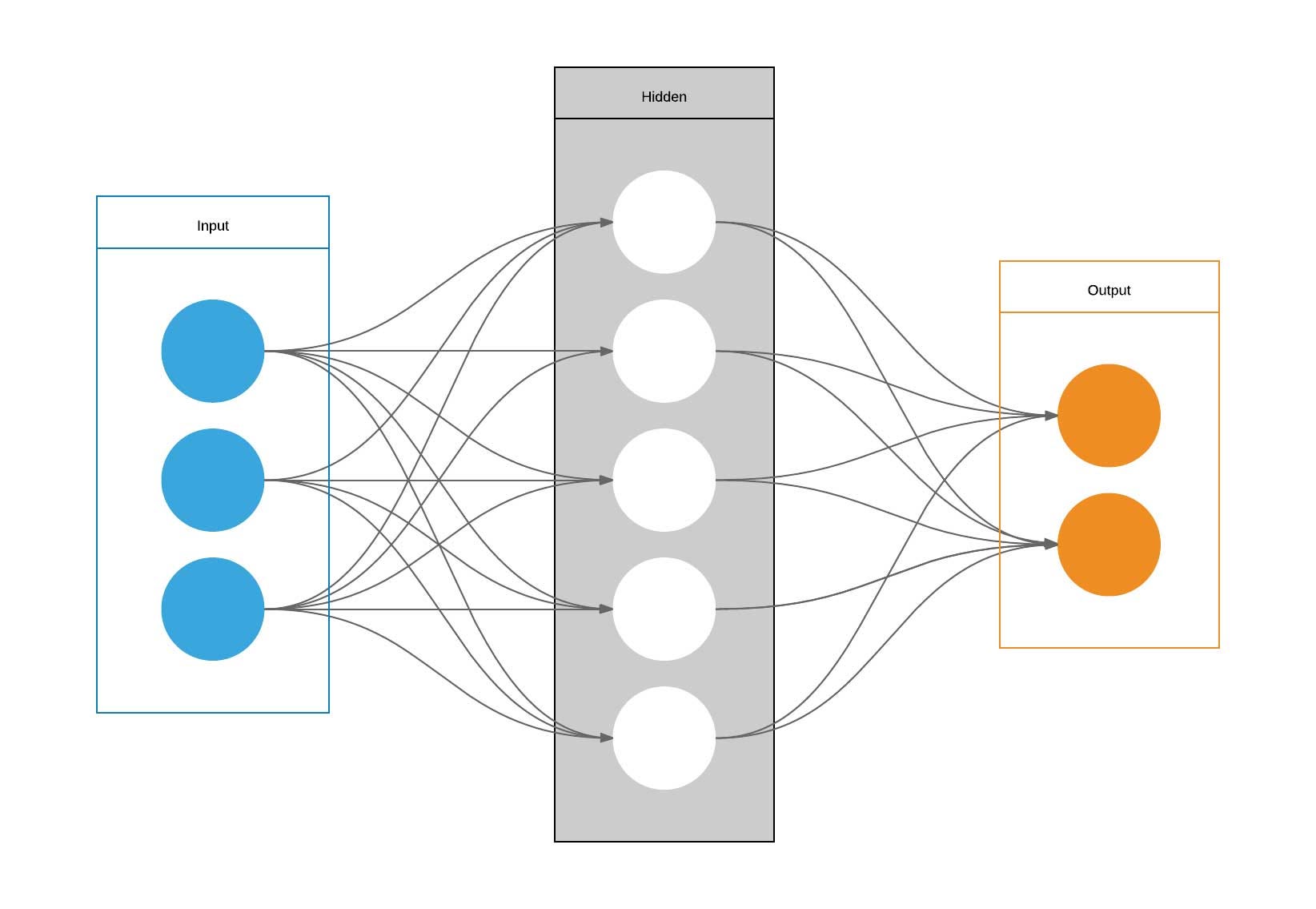图片来源：Wikimedia Commons

神经网络是一组旨在识别给定训练数据中趋势/关系的算法。这些算法基于人类神经元处理信息的方式。

下图公式展示了神经网络如何在每一层处理输入数据，并最终生成预测输出值。

$\hat{y} = \sigma(w^T x + b)$

训练过程是指模型建立训练数据与输出之间映射关系的过程。在此过程中，神经网络会更新其超参数，即权重 $w^T$ 和偏置 $b$ ，以满足上述公式。

每个训练输入通过一个称为前向传播（forward propagation）的过程被加载到神经网络中。一旦模型生成了输出，该预测输出就会与给定的目标输出进行比较，这一过程称为反向传播（backpropagation）——随后模型的超参数会被调整，使其输出结果更接近目标输出。

这正是损失函数发挥作用的地方。

图片来源：Wikimedia Commons

损失函数概述

损失函数是一种用于比较目标值与预测输出值的函数；它衡量神经网络对训练数据建模的好坏程度。在训练过程中，我们的目标是最小化预测输出与目标输出之间的损失。

模型的超参数会被调整，以最小化平均损失——我们寻找使损失函数 $J$ （即平均损失）取值最小的权重 $w^T$ 和偏置 $b$ 。

$J(w^T, b) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})$

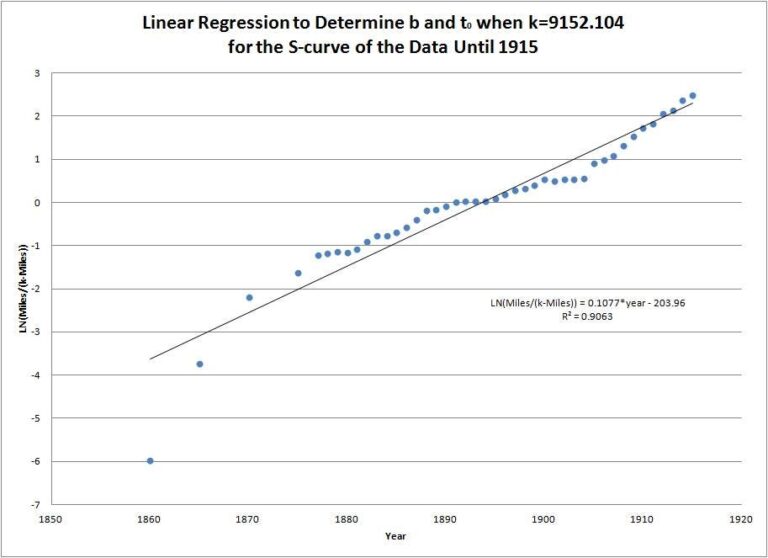
我们可以将其类比于统计学中的残差（residuals），残差衡量实际 y 值与回归线（预测值）之间的距离——目标是使总距离最小化。

图片来源：Wikimedia Commons

损失函数在 TensorFlow 中的实现

在本文中，我们将使用 Google 的 TensorFlow 库来实现不同的损失函数——这能清晰地展示损失函数在模型中的使用方式。

在 TensorFlow 中，神经网络使用的损失函数作为参数在 model.compile() 方法中指定——这是训练神经网络的最后一步。

model.compile(loss='mse', optimizer='sgd')

损失函数既可以以字符串形式传入（如上所示），也可以作为函数对象传入——该函数对象可以是从 TensorFlow 导入的，也可以是我们后面将讨论的自定义损失函数。

from tensorflow.keras.losses import mean_squared_error
model.compile(loss=mean_squared_error, optimizer='sgd')

TensorFlow 中的所有损失函数都具有类似的结构：

def loss_function(y_true, y_pred): 
    return losses

必须采用这种格式，因为 model.compile() 方法的 loss 参数只接受两个输入参数。

损失函数的类型

在监督学习中，主要有两种类型的损失函数——它们分别对应于两类主要的神经网络：回归损失函数和分类损失函数。

回归损失函数：用于回归神经网络；给定一个输入值，模型预测一个对应的输出值（而非预设的标签）。例如：均方误差（MSE）、平均绝对误差（MAE）。
分类损失函数：用于分类神经网络；给定一个输入，神经网络生成一个概率向量，表示该输入属于各个预设类别的概率——然后选择概率最高的类别作为最终输出。例如：二元交叉熵（Binary Cross-Entropy）、多分类交叉熵（Categorical Cross-Entropy）。

均方误差（Mean Squared Error, MSE）

MSE 是最流行的损失函数之一，它计算目标值与预测输出值之间差值的平方的平均值。

$MSE = \frac{1}{n} \sum_{i=1}^{n} (y^{(i)} - \hat{y}^{(i)})^2$

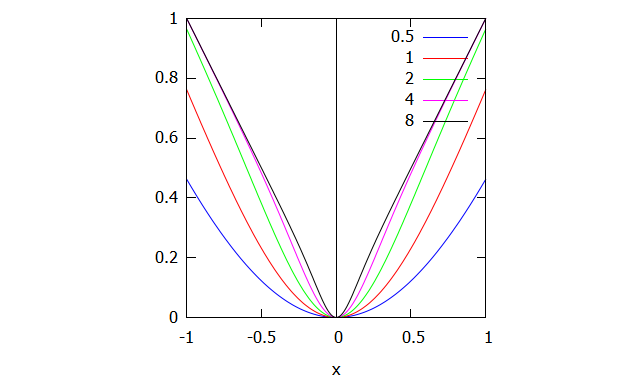
该函数具有多个特性，使其特别适合用于计算损失。差值被平方，这意味着无论预测值高于还是低于目标值都无关紧要；但误差较大的值会被显著惩罚。MSE 还是一个凸函数（如上图所示），具有明确的全局最小值——这使我们更容易利用梯度下降优化来设置权重值。

以下是 TensorFlow 中的标准实现——该函数也已内置于 TensorFlow 库中。

def mse(y_true, y_pred): 
    return tf.square(y_true - y_pred)

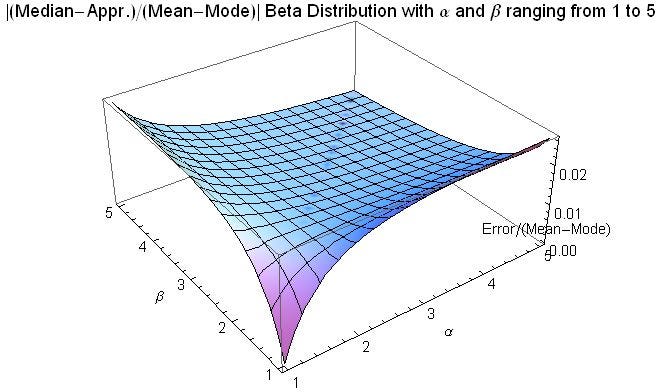
然而，该损失函数的一个缺点是它对异常值非常敏感；如果某个预测值显著大于或小于其目标值，这将大幅增加损失。

图片来源：Wikimedia Commons

平均绝对误差（Mean Absolute Error, MAE）

MAE 计算目标值与预测输出值之间绝对差值的平均值。

$MAE = \frac{1}{n} \sum_{i=1}^{n} |y^{(i)} - \hat{y}^{(i)}|$

该损失函数在某些情况下被用作 MSE 的替代方案。如前所述，MSE 对异常值高度敏感，因为距离被平方后会显著影响损失。当训练数据中存在大量异常值时，MAE 可用于缓解这一问题。

以下是 TensorFlow 中的标准实现——该函数也已内置于 TensorFlow 库中。

def mae(y_true, y_pred): 
    return tf.abs(y_true - y_pred)

但它也有一些缺点：当平均距离趋近于 0 时，梯度下降优化将无法工作，因为该函数在 0 处的导数未定义（这将导致错误，因为无法除以 0）。

因此，人们开发了一种名为 Huber Loss 的损失函数，它结合了 MSE 和 MAE 的优点。

\text{Huber Loss} = \begin{cases} \displaystyle \frac{1}{n} \sum_{i=1}^{n} (y^{(i)} - \hat{y}^{(i)})^2, & |y^{(i)} - \hat{y}^{(i)}| \leq \delta \\ \displaystyle \frac{1}{n} \sum_{i=1}^{n} \delta(|y^{(i)} - \hat{y}^{(i)}| - \frac{1}{2}\delta), & |y^{(i)} - \hat{y}^{(i)}| > \delta \end{cases}

如果实际值与预测值之间的绝对差值小于或等于某个阈值 $\delta$ ，则应用 MSE；否则（即误差足够大时），应用 MAE。

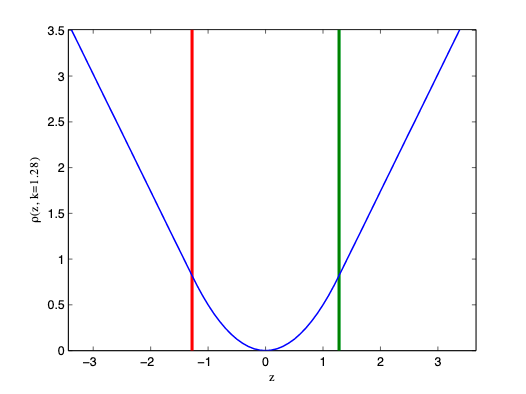图片来源：Wikimedia Commons

这是 TensorFlow 中的实现——这需要使用一个包装函数来利用阈值变量，我们稍后会讨论这一点。

def huber_loss_with_threshold(t=𝛿): 
    def huber_loss(y_true, y_pred): 
        error = y_true - y_pred 
        within_threshold = tf.abs(error) <= t
        small_error = tf.square(error)
        large_error = t * (tf.abs(error) - (0.5*t))
        if within_threshold: 
            return small_error
        else: 
            return large_error
    return huber_loss

二元交叉熵 / 对数损失（Binary Cross-Entropy / Log Loss）

这是用于二元分类模型的损失函数——模型接收一个输入，并将其分类为两个预设类别之一。

$\text{CE Loss} = \frac{1}{n} \sum_{i=1}^{N} - \left( y_i \cdot \log(p_i) + (1 - y_i) \cdot \log(1 - p_i) \right)$

分类神经网络通过输出一个概率向量来工作——表示给定输入属于各个预设类别的概率；然后选择概率最高的类别作为最终输出。

在二元分类中，y 的实际值只有两种可能：0 或 1。因此，为了准确确定实际值与预测值之间的损失，需要将实际值（0 或 1）与输入属于该类别的概率进行比较（ $p(i)$ = 属于类别 1 的概率；$ 1 - p(i) $ = 属于类别 0 的概率）。

这是 TensorFlow 中的实现：

def log_loss(y_true, y_pred): 
    y_pred = tf.clip_by_value(y_pred, 1e-7, 1 - 1e-7)
    error = y_true * tf.log(y_pred + 1e-7) + (1 - y_true) * tf.log(1 - y_pred + 1e-7)
    return -error

多分类交叉熵损失（Categorical Cross-Entropy Loss）

当类别数量大于二时，我们使用多分类交叉熵——其过程与二元交叉熵非常相似。

$\text{CE Loss} = -\frac{1}{n} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij} \cdot \log(p_{ij})$

二元交叉熵是多分类交叉熵的一种特殊情况，其中 $M = 2$ （即类别数为 2）。

自定义损失函数

如前所述，在编写神经网络时，可以从 tf.keras.losses 模块导入损失函数作为函数对象。该模块包含以下内置损失函数：

Kullback-Leibler (KL) divergence loss
Mean Absolute Error (MAE)
Mean Absolute Percentage Error (MAPE)
Mean Squared Error (MSE)
Mean Squared Logarithmic Error (MSLE)
Binary Crossentropy Loss
Binary Focal Crossentropy Loss
Sparse Categorical Crossentropy Loss
Categorical Hinge Loss
Hinge Loss
Cosine Similarity
Logcosh
Huber loss
Poisson loss

然而，在某些情况下，这些传统的主流损失函数可能不够用。例如，当训练数据中存在过多噪声（异常值、错误属性值等）且无法通过数据预处理补偿时，或用于无监督学习（我们稍后会讨论）时。在这些情况下，你可以编写自定义损失函数以适应特定条件。

def custom_loss_function(y_true, y_pred): 
    return losses

编写自定义损失函数非常简单；唯一的要求是损失函数必须仅接受两个参数：y_pred（预测输出）和 y_true（实际输出）。

以下是三个自定义损失函数的例子，适用于变分自编码器（VAE）模型，引自 Soon Yau Cheong 所著《Hands-On Image Generation with TensorFlow》：

def vae_kl_loss(y_true, y_pred):
    kl_loss = -0.5 * tf.reduce_mean(1 + vae.logvar - tf.square(vae.mean) - tf.exp(vae.logvar))
    return kl_loss

def vae_rc_loss(y_true, y_pred):
    # rc_loss = tf.keras.losses.binary_crossentropy(y_true, y_pred)
    rc_loss = tf.keras.losses.MSE(y_true, y_pred)
    return rc_loss

def vae_loss(y_true, y_pred):
    kl_loss = vae_kl_loss(y_true, y_pred)
    rc_loss = vae_rc_loss(y_true, y_pred)
    kl_weight_const = 0.01
    return kl_weight_const * kl_loss + rc_loss

根据损失函数的数学表达式，你可能需要添加额外参数——例如 Huber Loss 中的阈值 $ \delta $；为此，你必须包含一个包装函数，因为 TensorFlow 不允许损失函数拥有超过两个参数。

def custom_loss_with_threshold(threshold=1): 
    def custom_loss(y_true, y_pred): 
        pass  # 实现损失函数——可以调用 threshold 变量
    return custom_loss

在图像处理中的实现

让我们来看一些损失函数的实际应用。具体而言，我们将探讨损失函数如何用于处理各种用例中的图像数据。

图像分类

计算机视觉最基本的任务之一是图像分类——能够将图像分配到两个或多个预设标签之一；这使用户能够识别图像中的物体、文字、人物等（在图像分类中，图像通常只有一个主体）。

图像分类中最常用的损失函数是交叉熵损失/对数损失（二分类使用 binary crossentropy，三类及以上使用 sparse categorical crossentropy），模型输出一个概率向量，表示输入图像属于各个预设类别的概率。该输出随后与实际输出进行比较，实际输出由一个相同大小的向量表示，其中正确类别的概率为 1，其余为 0。

这种基础实现可以直接从 TensorFlow 库导入，无需进一步定制或修改。以下是一个 IBM 开源的深度卷积神经网络（CNN）的代码片段，用于对文档图像（身份证、申请表等）进行分类：

model.add(Dense(5, activation='sigmoid'))
model.summary()
model.compile(optimizer='adam', loss='categorical_crossentropy',
              metrics=['accuracy'])

目前，研究人员正在开发新的（自定义）损失函数以优化多分类任务。以下是杜克大学研究人员提出的一种损失函数的代码片段，该函数通过分析错误结果中的模式来扩展多分类交叉熵损失，从而加速学习过程。

def matrix_based_crossentropy(output, target, matrixA, from_logits=False):
    Loss = 0
    ColumnVector = np.matmul(matrixA, target)
    for i, y in enumerate(output):
        Loss -= (target[i] * math.log(output[i], 2))
        Loss += ColumnVector[i] * exponential(output[i])
        Loss -= (target[i] * exponential(output[i]))
    newMatrix = updateMatrix(matrixA, target, output, 4)
    return [Loss, newMatrix]

图像生成

图像生成是指神经网络根据用户指定的条件（从现有库中）创建图像的过程。

在本文中，我们主要讨论了损失函数在监督学习中的使用——在这种情况下，我们有明确标注的输入 $x$ 和输出 $y$ ，模型需要确定这两个变量之间的关系。

图像生成则是无监督学习的一种应用——模型需要分析并发现未标注输入数据集中的模式。损失函数的基本原理仍然适用；在无监督学习中，损失函数的目标是确定输入样本与其假设（即模型对输入样本本身的近似）之间的差异。

例如，以下公式展示了在无监督学习中如何实现 MSE，其中 $h(x)$ 是假设函数。

$L(h(x), x) = \frac{1}{n} \sum_{i=1}^{n} (h(x)^{(i)} - x^{(i)})^2$

以下是一个对比语言-图像预训练（CLIP）扩散模型的代码片段——该模型通过文本描述生成艺术图像（图片），并附带几个图像样本。

if args.init_weight:
    result.append(F.mse_loss(z, z_orig) * args.init_weight / 2)
lossAll, img = ascend_txt()
if i % args.display_freq == 0:
    checkin(i, lossAll)
loss = sum(lossAll)
loss.backward()

图片来源：作者

我们在“自定义损失函数”一节中提到的变分自编码器（VAE）模型，是损失函数在图像生成中应用的另一个例子。

总结

在本文中，我们涵盖了以下内容：

损失函数的工作原理
它们在神经网络中的应用方式
适用于特定神经网络的不同类型损失函数
两种具体损失函数及其使用场景
如何编写自定义损失函数
损失函数在图像处理中的实际实现