使用 scikit-learn 在 Python 中实现多项式回归（附实战示例）

Tamas Ujhelyi

如果你想使用 scikit-learn 对数据拟合一条曲线，那么你来对地方了！不过首先，请确保你已经熟悉线性回归。在本文中，我也默认你已经安装了 matplotlib、pandas 和 numpy。现在，让我们开始编写你的第一个多项式回归模型吧！

多项式回归有什么用？快速示例

坏消息：你不能对每个数据集都用线性回归搞定。😔

很多时候，你会遇到这样的数据：特征（feature）与响应变量（response variable）之间的关系无法用一条直线很好地描述。

就像下面这样：

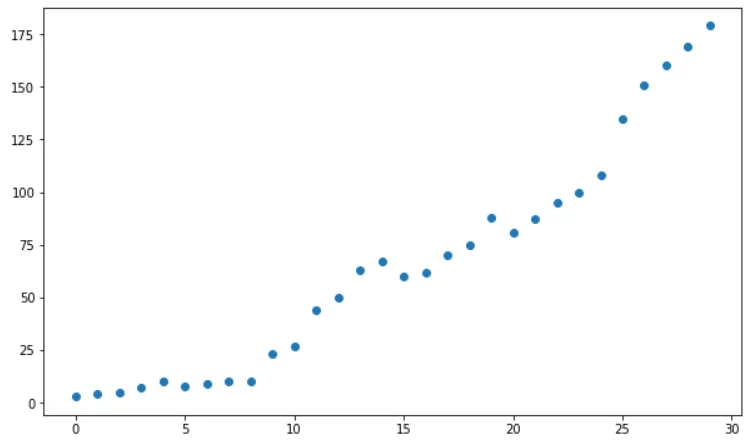
看到问题了吗？当然，我们可以强行拟合一条直线，但仅凭散点图我们就能感觉到：这次线性直线可能行不通。

如果你觉得这条线应该有点弯曲才能更好地拟合数据，那么你已经直观地理解了为什么我们要使用多项式回归：它能提供我们需要的曲率，从而基于数据做出更精确的预测。

不过，先别急着动手。🐴

为什么叫“多项式”？

这就是我们下一节要探讨的内容。

什么是多项式？你需要了解的最重要定义

我们来拆解一下：

• “poly” 意思是“多个”，
• “nomial” 意思是“项”（或“部分”、“名称”）。

举个多项式的例子：

$$4x + 7$$

4x + 7 是一个简单的数学表达式，包含两个项：4x（第一项）和 7（第二项）。在代数中，项由逻辑运算符 + 或 - 分隔，因此你可以轻松数出一个表达式有多少项。

9x²y - 3x + 1 也是一个多项式（包含 3 项）。为了让你更困惑一点，3x 也是多项式，尽管它没有“很多项”（3x 被称为单项式 monomial，因为它只包含一项——不过别太担心这个，我只是想悄悄告诉你这个小秘密 🤫）。

现在，我们先专注于 4x + 7。我为你画出了它的图像：

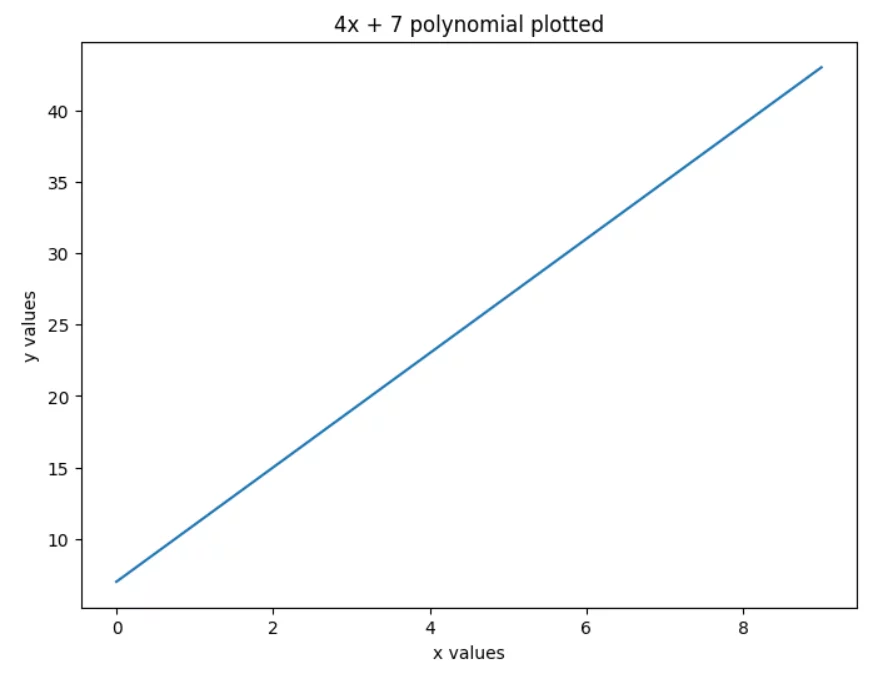
现在请你仔细观察这张图——你看到了什么？一条直线！😮

让我们回顾一下刚才发生了什么：

• 我们取了一个多项式（4x + 7），
• 绘制了它，
• 得到了一条直线（记住：线性回归模型给出的就是一条直线）。

这是怎么回事？🤔

其实，线性回归模型中定义直线的公式本身就是一个多项式，它还有个特殊的名字：一次多项式（任何形如 ax + b 的表达式都是一次多项式）。

很好！那我们现在可以开始编码了吗？

实际上……还不行。

多项式回归相关术语

在进入实践部分之前，还有一些内容你需要了解。

我们用 3x⁴ – 7x³ + 2x² + 11 来提升你关于多项式的词汇量，并学习一些关键定义：

• 多项式的次数（degree of a polynomial）：多项式中最高次幂（最大指数）；在我们的例子中是 4（因为 x⁴），这意味着我们处理的是一个四次多项式。
• 系数（coefficient）：多项式中的每个数字（3、7、2、11）都是系数；这些是我们多项式回归模型在训练时试图估计的未知参数。
• 首项（leading term）：次数最高的项（在我们的例子中是 3x⁴）；这是多项式中最重要的部分，因为它决定了多项式图像的行为。
• 首项系数（leading coefficient）：首项的系数（在我们的例子中是 3）。
• 常数项（constant term）：y 轴截距，它永远不会改变：无论 x 取何值，常数项始终保持不变。

多项式回归：官方定义

既然你已经掌握了正确的多项式术语，我想给你一个正式的定义：

一个表达式是多项式，当且仅当：

• 表达式包含有限数量的项，
• 每一项都有一个系数，
• 这些系数乘以一个变量（在我们的例子中是 x），
• 并且变量的指数是非负整数。

如果你一直认真听讲，可能会疑惑：4x + 7 明明第二项（7）没有变量 x，为什么也算多项式？

其实，x 是存在的，形式为 7x⁰。由于 x⁰ = 1，而 7×1 = 7，所以根本没必要写下 x⁰。

线性回归与多项式回归的区别

再回到 3x⁴ - 7x³ + 2x² + 11：如果我们按从高次到低次的顺序书写多项式的项，这被称为多项式的标准形式。

在机器学习中，你经常会看到它被反过来写：

y = ß₀ + ß₁x + ß₂x² + … + ßₙxⁿ

其中：

• y 是我们想要预测的响应变量，
• x 是特征，
• ß₀ 是 y 轴截距，
• 其他 ß 是我们在模型训练时希望找到的系数/参数，
• n 是多项式的次数（n 越高，你能创建的曲线就越复杂）。

上面的多项式回归公式与多元线性回归公式非常相似：

y = ß₀ + ß₁x₁ + ß₂x₂ + … + ßₙxₙ

这并非巧合：多项式回归是一种线性模型，用于描述非线性关系。

这怎么可能？奥秘在于通过将原始特征提升到不同次幂来创建新特征。

例如，如果我们有一个特征 x，并使用三次多项式，那么我们的公式还会包括 x² 和 x³。正是这一点赋予了直线曲率：

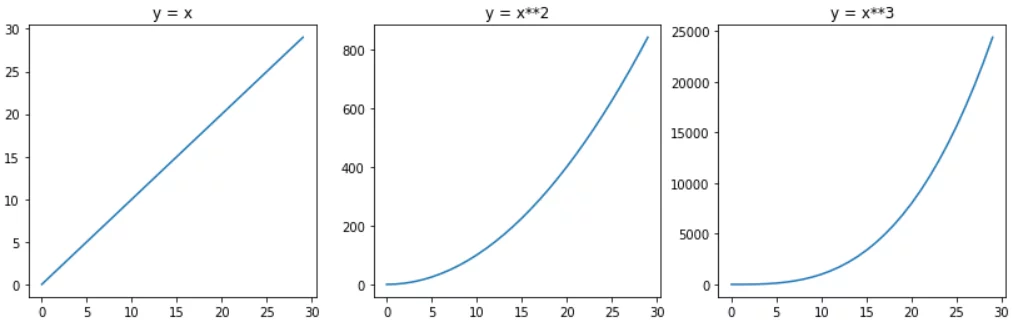
我想强调的是：线性回归只是一次多项式。多项式回归使用更高次的多项式。两者都是线性模型，但前者产生直线，后者产生曲线。仅此而已。

现在，你已经准备好编写你的第一个多项式回归模型了！

使用 scikit-learn 编写多项式回归模型

假设你面对如下散点图：

你可以用以下代码复现这张图：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

x = np.arange(0, 30)
y = [3, 4, 5, 7, 10, 8, 9, 10, 10, 23, 27, 44, 50, 63, 67, 60, 62, 70, 75, 88, 81, 87, 95, 100, 108, 135, 151, 160, 169, 179]

plt.figure(figsize=(10,6))
plt.scatter(x, y)
plt.show()

这没什么特别的：只有一个特征（x）和对应的响应值（y）。

现在，假设你怀疑特征与响应之间的关系是非线性的，你想拟合一条曲线。

因为我们只有一个特征，所以适用以下多项式回归公式：

y = ß₀ + ß₁x + ß₂x² + … + ßₙxⁿ

在这个方程中，系数（ß）的数量由特征的最高次幂（即多项式的次数，不包括截距 ß₀）决定。

立刻会冒出两个问题：

1. 我们如何确定多项式的次数（从而确定 ß 的数量）？
2. 当我们最初只有一个特征 x 时，如何创建 x²、x³ 或 xⁿ？

幸运的是，这两个问题都有答案。

答案 1：有方法可以确定使结果最佳的多项式次数，稍后我们会讨论。现在，我们先假设数据可以用二次多项式描述。

答案 2：一旦你安装了 scikit-learn，就可以创建这些新特征。

步骤 #1：确定多项式的次数

首先，导入 PolynomialFeatures：

from sklearn.preprocessing import PolynomialFeatures

然后创建一个 PolynomialFeatures 实例，并设置如下参数：

poly = PolynomialFeatures(degree=2, include_bias=False)

• degree 设置多项式函数的次数。degree=2 表示我们使用二次多项式：

  y = ß₀ + ß₁x + ß₂x²

• include_bias=False 应设为 False，因为我们稍后会与 LinearRegression() 一起使用 PolynomialFeatures。

简单来说：LinearRegression() 默认会处理截距项，所以我们不需要在这里设置 include_bias=True。如果不这样处理，include_bias=False 就意味着我们故意让 y 截距（ß₀）等于 0——但我们并不希望这样。这里有一篇很好的解释。

如果你打印 poly，你会发现目前我们只是创建了一个 PolynomialFeatures 实例，仅此而已：

PolynomialFeatures(degree=2, include_bias=False)
poly
PolynomialFeatures(include_bias=False)

进入下一步：

步骤 #2：创建新特征

poly_features = poly.fit_transform(x.reshape(-1, 1))

reshape(-1,1) 将我们的 numpy 数组 x 从一维数组转换为二维数组——这是必需的，否则你会得到如下错误：

ValueError: Expected 2D array, got 1D array instead:

虽然这里只用了一个方法 fit_transform()，但它实际上是两个独立方法的组合：fit() 和 transform()。fit_transform() 是同时使用两者的快捷方式，因为它们经常一起使用。

为了让你理解底层发生了什么，我会分别展示它们。

• fit() 基本上只是声明我们要转换哪些特征：

• transform() 执行实际的转换：

这些数字是什么？让我提醒你：我们的散点图中特征值范围是 0 到 29。第一列是 x 的值（例如 3），第二列是 x 的平方值（例如 9）。

眼熟吗？再次回顾我们的二次多项式公式：

y = ß₀ + ß₁x + ß₂x²

我们想从 x 创建 x²，而 fit_transform() 正好完成了这项工作。我们将结果保存到 poly_features：

poly_features = poly.fit_transform(x.reshape(-1, 1))

步骤 #3：创建多项式回归模型

现在是时候创建我们的机器学习模型了。当然，首先要导入它：

from sklearn.linear_model import LinearRegression

等等！😮 这不是多项式回归教程吗？为什么导入的是 LinearRegression？

回想一下你不久前读过的内容：多项式回归是一种线性模型，所以我们导入 LinearRegression。🙂

将 LinearRegression 的一个实例保存到变量中：

poly_reg_model = LinearRegression()
poly_reg_model
LinearRegression()

然后用我们的数据拟合模型：

poly_reg_model.fit(poly_features, y)

“拟合”意味着我们通过提供特征（poly_features）和响应值（y）来训练模型。在拟合/训练过程中，我们实际上是在指示模型求解多项式函数中的系数（加粗显示）：

y = ß₀ + ß₁x + ß₂x²

运行代码后你可能觉得什么都没发生，但相信我，模型已经估算了系数（重要提示：你不需要将其保存到变量中，它也能正常工作！）：

poly_reg_model.fit(poly_features, y)
LinearRegression()

现在模型已经训练好了，我们可以让它根据 poly_features 和估算出的系数来预测响应值（y_predicted）：

y_predicted = poly_reg_model.predict(poly_features)

以下是预测的响应值：

让我们做一些数据可视化，看看模型长什么样：

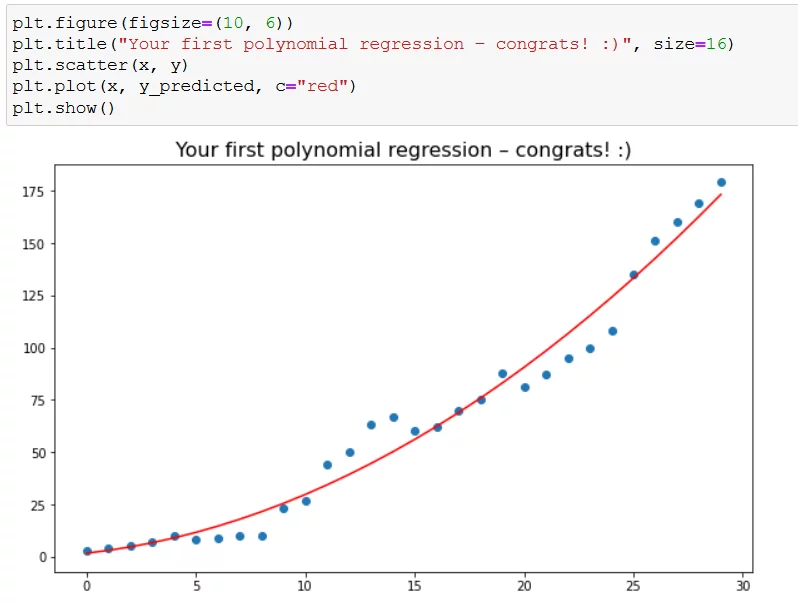
我觉得图的标题已经说明了一切，但我还是要重复一遍：恭喜你，你创建了你的第一个多项式回归模型！👏

在你庆祝的同时，我把完整代码贴在这里，方便你使用：

plt.figure(figsize=(10, 6))
plt.title("Your first polynomial regression – congrats! :)", size=16)
plt.scatter(x, y)
plt.plot(x, y_predicted, c="red")
plt.show()

使用多个特征编写多项式回归模型

很多时候，你需要处理包含多个特征的数据（生活很复杂，我知道）。让我们模拟这种情况：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

np.random.seed(1)
x_1 = np.absolute(np.random.randn(100, 1) * 10)
x_2 = np.absolute(np.random.randn(100, 1) * 30)
y = 2*x_1**2 + 3*x_1 + 2 + np.random.randn(100, 1)*20

np.random.seed(1) 确保你和我使用相同的“随机”数据。（如果你想了解这是如何实现的，请阅读这篇文章。）我们创建了一些带噪声的随机数据：x_1 包含第一个特征的 100 个值，x_2 包含第二个特征的 100 个值。响应值（100 个）保存在 y 中。

让我们绘制两个特征，直观理解特征与响应之间的关系：

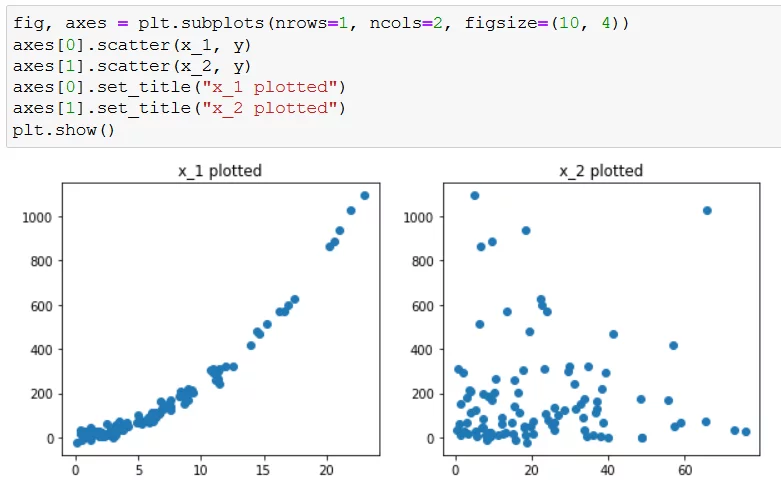
为方便起见，这里是代码：

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axes[0].scatter(x_1, y)
axes[1].scatter(x_2, y)
axes[0].set_title("x_1 plotted")
axes[1].set_title("x_2 plotted")
plt.show()

步骤 #1：将变量存储在 DataFrame 中

然后我们创建一个 pandas DataFrame 来存储特征和响应：

df = pd.DataFrame({
    "x_1": x_1.reshape(100,),
    "x_2": x_2.reshape(100,),
    "y": y.reshape(100,)
}, index=range(0,100))
df

这是生成的 DataFrame：

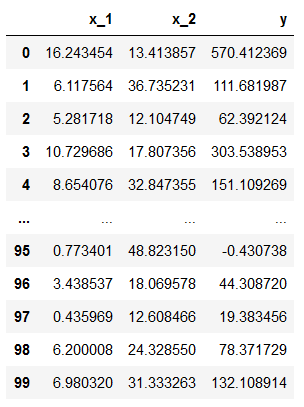
同样，reshape(100,) 是必需的（因为我们有 100 行），否则你会收到如下错误：

Exception: Data must be 1-dimensional

步骤 #2：定义训练集和测试集

现在我们再次转向 scikit-learn：

from sklearn.model_selection import train_test_split

train_test_split 帮助我们将数据分为训练集和测试集：

X, y = df[["x_1", "x_2"]], df["y"]
poly = PolynomialFeatures(degree=2, include_bias=False)
poly_features = poly.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(poly_features, y, test_size=0.3, random_state=42)

逐步解释：

• X, y = df[["x_1", "x_2"]], df["y"]：从 df 中，我们将 x_1 和 x_2 列保存到 X，将 y 列保存到 y。此时，特征和响应已分别存储在不同变量中。
• poly = PolynomialFeatures(...) 和 poly_features = poly.fit_transform(X)：和之前一样，我们创建新的多项式特征。
• train_test_split(..., test_size=0.3, random_state=42)：
  • test_size=0.3 表示我们将 30% 的数据用于测试（这是良好实践）。
  • random_state=42 确保每次运行结果一致。
• X_train, X_test, y_train, y_test：train_test_split 将特征和响应分为训练组和测试组——我们将其保存到变量中。变量顺序非常重要，不要打乱。

步骤 #3：创建多项式回归模型

现在创建并拟合模型，但这次只在训练数据上训练：

poly_reg_model = LinearRegression()
poly_reg_model.fit(X_train, y_train)

我们只在训练数据上训练模型，是为了之后评估模型对未见过数据的预测能力。

测试模型在新数据上的表现：

poly_reg_y_predicted = poly_reg_model.predict(X_test)

from sklearn.metrics import mean_squared_error
poly_reg_rmse = np.sqrt(mean_squared_error(y_test, poly_reg_y_predicted))
poly_reg_rmse

这可能信息量很大，让我详细解释：

• poly_reg_y_predicted = ...：保存模型基于未见过的特征（X_test）预测的值。
• from sklearn.metrics import mean_squared_error：导入均方误差（MSE）。
• poly_reg_rmse = np.sqrt(...)：取 MSE 的平方根得到 RMSE（均方根误差），这是评估机器学习模型性能的常用指标。RMSE 表示模型预测值与真实值之间的平均偏差。RMSE 越小，模型越好。

如果你打印 poly_reg_rmse，会得到这个数值：

poly_reg_rmse
20.937707839078772

步骤 #4：创建线性回归模型

现在我们也创建一个线性回归模型，以便比较两种模型的性能：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

lin_reg_model = LinearRegression()
lin_reg_model.fit(X_train, y_train)
lin_reg_y_predicted = lin_reg_model.predict(X_test)
lin_reg_rmse = np.sqrt(mean_squared_error(y_test, lin_reg_y_predicted))
lin_reg_rmse

步骤与多项式回归模型相同，但有一个重要区别：在 train_test_split 中我们使用 X 而不是 poly_features，原因如下。

X 包含两个原始特征（x_1 和 x_2），因此线性回归模型形式为：

y = ß₀ + ß₁x₁ + ß₂x₂

如果你打印 lin_reg_model.coef_，可以看到 ß₁ 和 ß₂ 的值：

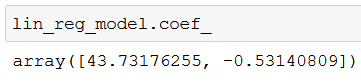
你也可以用 lin_reg_model.intercept_ 打印截距。

另一方面，poly_features 包含由 x_1 和 x_2 生成的新特征，因此我们的多项式回归模型（基于两个特征的二次多项式）形式如下：

y = ß₀ + ß₁x₁ + ß₂x₂ + ß₃x₁² + ß₄x₂² + ß₅x₁x₂

这是因为 poly.fit_transform(X) 在原始两个特征（x₁ 和 x₂）基础上新增了三个特征：x₁²、x₂² 和 x₁x₂。

• x₁² 和 x₂² 无需解释，前文已覆盖。
• x₁x₂ 更有趣——当两个特征相乘时，称为交互项（interaction term）。交互项考虑了一个变量的值可能依赖于另一个变量的值（更多解释）。poly.fit_transform() 自动为我们创建了这个交互项，是不是很酷？🙂

相应地，如果你打印 poly_reg_model.coef_，会得到五个系数（ß₁ 到 ß₅）的值：

但让我们回到模型性能比较：打印 lin_reg_rmse：

lin_reg_rmse
62.302487453878506

多项式回归模型的 RMSE 是 20.94（约），而线性回归模型的 RMSE 是 62.3（约）。多项式回归模型的性能几乎是线性回归模型的 3 倍！这是一个惊人的差距。

但你知道还有什么更惊人吗？

你刚刚获得的关于执行多项式回归的新知识！😉

结论

希望你现在已经掌握了多项式回归的基本知识。不仅如此，你还学会了比较机器学习模型性能的一种方法（RMSE）。

在本文中，我们使用了二次多项式。当然，在部署模型前，你应该始终测试哪种次数的多项式在你的数据集上表现最好（读完本文后，你应该已经猜到该怎么做了！😉）。

感谢阅读本文，祝你用新知识玩得开心！