概率分布 | 公式、类型与示例

Shaun Turney 2025-01-24

概率分布是一种数学函数，用于描述一个变量取不同可能值的概率。概率分布通常通过图形或概率表来表示。

示例：概率分布
我们可以使用概率表来描述一次抛硬币的概率分布：

结果	概率
正面	0.5
反面	0.5

常见的概率分布包括二项分布、泊松分布和均匀分布。某些类型的概率分布用于假设检验，包括标准正态分布、F 分布和学生 t 分布。

什么是概率分布？

概率分布是一种理想化的频数分布。

频数分布描述的是某个特定样本或数据集的情况，即变量的每个可能取值在该数据集中出现的次数。

一个值在样本中出现的次数由其出现的概率决定。概率是介于 0 和 1 之间的数字，表示某事发生的可能性：

0 表示不可能发生；
1 表示必然发生。

一个值的概率越高，它在样本中的频数就越高。

更具体地说，一个值的概率是在一个无限大的样本中其相对频率。

现实中无法获得无限大的样本，因此概率分布是理论性的。它们是频数分布的理想化版本，旨在描述样本所来自的总体。

概率分布用于描述现实生活中变量的总体，例如抛硬币的结果或鸡蛋的重量。它们也用于假设检验以确定 p 值。

示例：概率分布是理想化的频数分布
假设一位养鸡户想知道她农场产出的鸡蛋达到某种尺寸的概率。

她随机称量了 100 枚鸡蛋，并使用直方图描述其频数分布：

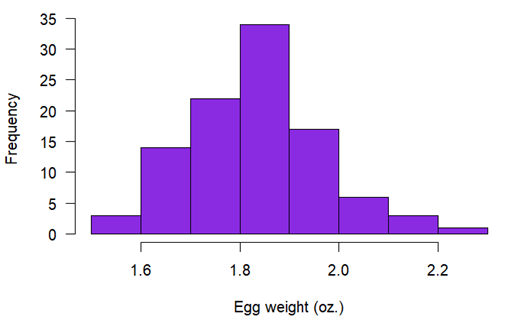
她可以直接从这个频数分布中大致了解不同鸡蛋尺寸的概率。例如，她可以看出鸡蛋重量约为 1.9 盎司的概率很高，而大于 2.1 盎司的概率很低。

假设这位农户希望获得更精确的概率估计。一种选择是称量更多的鸡蛋以改进估计。

更好的方法是认识到鸡蛋尺寸似乎遵循一种常见的概率分布——正态分布。农户可以通过假设鸡蛋重量服从正态分布，构建一个理想化的鸡蛋重量分布：

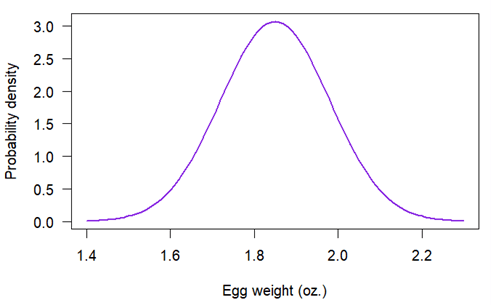
由于统计学家对正态分布已有深入理解，即使样本量相对较小，农户也可以计算出精确的概率估计。

遵循概率分布的变量称为随机变量。你可以使用特定符号表示一个随机变量服从某种特定分布：

随机变量通常用 X 表示；
$\sim$ （波浪号）表示“服从……分布”；
分布用大写字母表示（通常是分布名称的首字母），括号内包含该分布的参数。

例如，以下符号表示：“随机变量 X 服从均值为 µ、方差为 σ² 的正态分布。”

X \sim N(\mu,\sigma^2)

概率分布分为两类：

离散概率分布
连续概率分布

离散概率分布

离散概率分布是分类变量或离散变量的概率分布。

离散概率分布只包含可能出现的值的概率。换句话说，离散概率分布不包括概率为零的值。例如，掷骰子的概率分布不包括 2.5，因为这不是骰子可能出现的结果。

离散概率分布中所有可能值的概率之和为 1。也就是说，观察值必然是某个可能值之一（即概率为 1）。

概率表

概率表表示分类变量的离散概率分布。概率表也可用于表示仅有少量可能取值的离散变量，或已被分组为区间类别的连续变量。

概率表由两列组成：

值或区间类别
对应的概率

示例：概率表
一个机器人使用随机问候语向人打招呼。问候语的概率分布如下表所示：

问候语	概率
“Greetings, human!”	0.6
“Hi!”	0.1
“Salutations, organic life-form.”	0.2
“Howdy!”	0.1

注意：所有概率都大于零，且总和为 1。

概率质量函数（PMF）

概率质量函数（Probability Mass Function, PMF）是一种描述离散概率分布的数学函数。它给出变量每个可能取值的概率。

概率质量函数可以表示为公式或图形。

示例：概率质量函数
假设美国每人拥有的毛衣数量服从泊松分布。

该分布的概率质量函数公式如下：

P(X = k) = \dfrac{e^{-\lambda} \lambda^k}{k!}

其中：

$P(X = k)$ 是一个人恰好拥有 $k$ 件毛衣的概率；
$\lambda$ 是每人平均拥有的毛衣数量（本例中 $\lambda = 3$ ）；
$e$ 是欧拉常数（约等于 2.718）。

此概率质量函数也可以用图形表示：

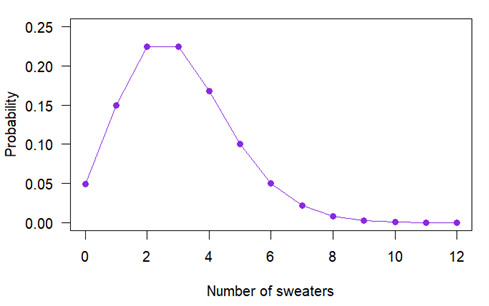
注意：变量只能取某些特定值，这些值用实心圆点表示。你可以拥有 2 件或 10 件毛衣，但不能拥有 3.8 件毛衣。

一个人拥有 0 件毛衣的概率是 0.05，拥有 1 件的概率是 0.15，依此类推。如果你将一个人可能拥有的所有毛衣数量的概率相加，总和正好等于 1。

常见的离散概率分布

分布	描述	示例
二项分布	描述具有两种可能结果的变量。它是 n 次试验中成功次数的概率分布，每次试验成功的概率为 p。	抛 5 次硬币正面朝上的次数
离散均匀分布	描述各事件具有相等概率的情况。	随机抽取一张扑克牌的花色
泊松分布	描述计数数据。给出在给定时间或空间间隔内某事件发生 k 次的概率。	每天收到的短信数量

连续概率分布

连续概率分布是连续变量的概率分布。

连续变量可以在其最小值和最大值之间取任意值。因此，连续概率分布包含变量取值范围内的每一个数值。

连续变量取某个特定值的概率极其微小，被认为概率为零。然而，该值落在其范围内某个区间内的概率大于零。

概率密度函数（PDF）

概率密度函数（Probability Density Function, PDF）是一种描述连续概率分布的数学函数。它提供变量每个取值的概率密度，该密度值可以大于 1。

概率密度函数可以表示为公式或图形。

以图形形式呈现时，概率密度函数是一条曲线。你可以通过计算曲线下某一区间内的面积，来确定该值落入该区间的概率。你可以使用参考表或软件来计算该面积。

整条曲线下面积始终恰好为 1，因为观察值必然落在变量的取值范围内（即概率为 1）。

累积分布函数（CDF）是另一种描述连续概率分布的函数。

示例：概率密度函数
鸡蛋重量服从正态分布，其概率密度函数公式如下：

f(x) = \dfrac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\dfrac{x-\mu}{\sigma}\right)^2}

其中：

$f(x)$ 是鸡蛋重量的概率密度；
$\mu$ 是总体中鸡蛋的平均重量（本例中 $\mu = 1.85$ 盎司）；
$\sigma$ 是总体中鸡蛋重量的标准差（本例中 $\sigma = 0.13$ 盎司）。

一枚鸡蛋重量恰好为 2 盎司的概率为零。尽管鸡蛋重量可能非常接近 2 盎司，但精确等于 2 盎司的可能性极低。即使普通秤显示鸡蛋重 2 盎司，无限精度的秤也会发现其与 2 盎司存在微小差异。

鸡蛋重量落在某个区间（如 1.98 至 2.04 盎司）内的概率大于零，可在概率密度函数图中表示为阴影区域：

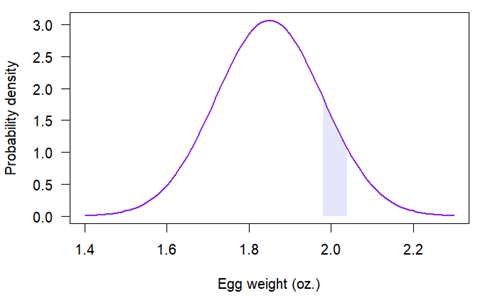
阴影区域面积为 0.09，表示鸡蛋重量在 1.98 至 2.04 盎司之间的概率为 0.09。该面积通过统计软件计算得出。

常见的连续概率分布

分布	描述	示例
正态分布	描述数据值偏离均值越远概率越低，其概率密度函数呈钟形。	SAT 考试成绩
连续均匀分布	描述等长区间具有相等概率的数据。	汽车在红灯前等待的时间
对数正态分布	描述右偏数据。它是对数服从正态分布的随机变量的概率分布。	不同哺乳动物物种的平均体重
指数分布	描述小值比大值更可能出现的数据。它是独立事件之间时间间隔的概率分布。	地震之间的时间间隔

如何计算期望值和标准差

如果你有分布的公式、样本或概率表，就可以计算该概率分布的期望值和标准差。

注意：名义变量没有期望值或标准差。

期望值是分布均值的另一个名称，通常写作 $E(x)$ 或 $\mu$ 。如果你从该分布中随机抽取一个样本，你应预期该样本的均值近似等于期望值。

如果你有描述分布的公式（如概率密度函数），期望值通常由参数 $\mu$ 给出。如果没有 $\mu$ 参数，则可使用针对每种分布的特定公式，通过其他参数计算期望值。
如果你有一个样本，那么该样本的均值就是总体概率分布期望值的估计值。样本量越大，估计越准确。
如果你有概率表，可通过将每个可能结果乘以其概率，然后求和来计算期望值。

示例：期望值
美洲知更鸟每窝产卵 2 到 4 枚。假设下表描述了每窝知更鸟卵数的概率分布：

卵数	概率
2	0.2
3	0.5
4	0.3

每窝知更鸟卵数的期望值是多少？

将每个可能结果乘以其概率：

卵数 (x)	概率 P(x)	x × P(x)
2	0.2	2 × 0.2 = 0.4
3	0.5	3 × 0.5 = 1.5
4	0.3	4 × 0.3 = 1.2

求和：

E(x) = 0.4 + 1.5 + 1.2 = 3.1 \text{ 枚卵}

标准差是衡量分布变异性的指标，通常写作 $\sigma$ 。

如果你有描述分布的公式（如概率密度函数），标准差有时由参数 $\sigma$ 给出。如果没有 $\sigma$ 参数，则通常可使用针对每种分布的特定公式，通过其他参数计算标准差。
如果你有一个样本，该样本的标准差就是总体概率分布标准差的估计值。样本量越大，估计越准确。
如果你有概率表，可通过以下步骤计算标准差：
1. 计算每个值与期望值的偏差；
2. 将偏差平方；
3. 乘以其概率；
4. 求和后开平方根。

示例：标准差

计算每个值与期望值的偏差：

卵数 (x)	概率 P(x)	x − E(x)
2	0.2	2 − 3.1 = −1.1
3	0.5	3 − 3.1 = −0.1
4	0.3	4 − 3.1 = 0.9

将偏差平方并乘以其概率：

卵数 (x)	概率 P(x)	x − E(x)	[x − E(x)]² × P(x)
2	0.2	−1.1	(−1.1)² × 0.2 = 0.242
3	0.5	−0.1	(−0.1)² × 0.5 = 0.005
4	0.3	0.9	(0.9)² × 0.3 = 0.243

求和并开平方根：

\sigma = \sqrt{0.242 + 0.005 + 0.243} = \sqrt{0.49} = 0.7 \text{ 枚卵}

如何使用零分布进行假设检验

零分布是假设检验中的重要工具。零分布是指当检验的零假设成立时，检验统计量的概率分布。

所有假设检验都涉及一个检验统计量。常见例子包括 z、t、F 和卡方（χ²）。检验统计量将样本汇总为一个单一数值，然后将其与零分布比较以计算 p 值。

p 值是在零假设成立的前提下，获得等于或比样本检验统计量更极端的值的概率。实际上，它是零分布概率密度函数曲线下等于或比样本检验统计量更极端部分的面积。

示例：使用零分布进行假设检验
单样本 t 检验是一种使用名为“学生 t”的检验统计量的假设检验。如果一个样本的 t 值为 1.7，我们通过计算零分布（学生 t 分布）中 t = 1.7 右侧的阴影面积（单侧检验）来得到 p 值：

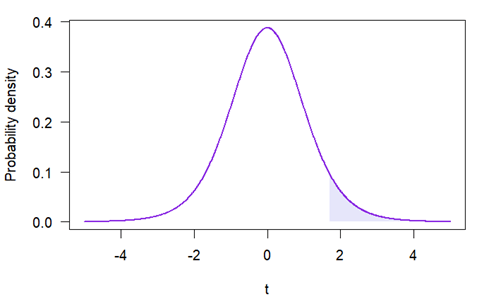
该面积可通过微积分、统计软件或参考表计算，结果为 0.06。因此，该样本的 p 值为 0.06。

常见零分布及其对应的统计检验

分布	统计检验
标准正态分布（z 分布）	单样本位置检验
学生 t 分布	单样本 t 检验双样本 t 检验配对 t 检验线性回归皮尔逊相关
F 分布	方差分析（ANOVA）嵌套线性模型比较两个方差相等性检验
卡方分布	卡方拟合优度检验卡方独立性检验 McNemar 检验单方差检验

概率分布公式

常见概率分布的概率质量函数和概率密度函数

分布	公式	公式类型
二项分布	$P(X = k) = \frac{n!}{k!(n - k)!} p^k (1 - p)^{n - k}$	概率质量函数
离散均匀分布	$P(X = x) = \frac{1}{b - a + 1}$	概率质量函数
泊松分布	$P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}$	概率质量函数
正态分布	$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2}$	概率密度函数
连续均匀分布	$f(x) = \begin{cases} \dfrac{1}{b - a} & ; a \leq x \leq b \\ 0 & ;\ x < a\ \text{or}\ x > b \end{cases}$	概率密度函数
指数分布	$f(x) = \begin{cases} \lambda e^{-\lambda x} & ;\ x \geq 0 \\ 0 & ;\ x < 0 \end{cases}$	概率密度函数