机器学习中的概率

Ajay Halthor 2022-09-12

1. 引言

在本文中，我们将逐步介绍概率论的基本构建模块，并利用这些知识来激发机器学习中的核心思想。第一部分将讨论随机变量及其如何帮助我们量化现实世界中的实验。接下来的部分将过渡到概率分布函数。最后一部分将讨论这些数学概念如何协同工作以解决机器学习问题。

2. 随机变量

让我们从一个有趣的实验开始我们的旅程。拿一支笔和一张纸；走到你家门前的主街上。观察每一个路过你的人，并记录下他们的发色、身高（以厘米为单位的大致估计值），以及你感兴趣的任何其他细节。持续进行大约10分钟。

恭喜！你完成了你的第一个实验！通过这个实验，你现在可以回答一些问题：有多少人从你身边走过？其中有多少人是蓝发？路过你的人的平均身高是多少？也许在这个实验中，有10个人从你身边走过；其中3个人是蓝发；他们估算的平均身高可能是165.32厘米。对于每个问题，我们都将其与某个数值联系起来；即与某个可测量的量联系起来。

随机变量是将实验结果映射到可测量量的函数。

现在，我们可以用随机变量来表示上述三个问题。例如，令 $X_1$ 为表示从你身边走过的人数的随机变量。注意，根据定义，随机变量是函数。因此，我们可以用函数记号写出如下内容：

公式 1
$$X_1(\text{从你身边走过的人数}) = 10$$

这意味着随机变量 $X_1$ 是一个将“从你身边走过的人数”（实验的一个结果）映射到某个非负整数10（一个可测量量）的函数。类似地，令 $X_2$ 为表示从你身边走过且拥有蓝发的人数的随机变量。那么我们可以写出如下内容：

公式 2
$$X_2(\text{从你身边走过且拥有蓝发的人数}) = 3$$

这意味着 $X_2$ 是一个将“从你身边走过且拥有蓝发的人数”（实验的一个结果）映射到非负整数3（一个可测量量）的函数。同样地，令 $X_3$ 为表示从你身边走过的人的平均身高的随机变量。

公式 3
$$X_3(\text{从你身边走过的人的平均身高}) = 165.32$$

这意味着 $X_3$ 是一个将“从你身边走过的人的平均身高”（实验的一个结果）映射到非负实数165.32（一个可测量量）的函数。使这些随机变量如此有用的是它们能够将观察人类的有趣实验转化为我们可以进行数学运算的数字。在下一节中，我们将看到这些随机变量如何构成概率分布函数的核心。

3. 概率分布函数

随机变量为我们提供了一种量化实验结果的方法。但这些结果（以及相应的随机变量）究竟是如何表现的呢？我们可以借助概率分布函数来理解这一点。

在我们的实验中，我们看到10个人经过我们。“10个人”就是一个“结果”的例子。然而，我们也可能看到0个人经过我们，或1个人，或2个人，依此类推。因此，该实验所有可能结果的集合 $S$ 如下所示：

公式 4
$$S = \{0人, 1人, 2人, 3人, \dots\}$$

这个可能结果的集合 $S$ 被称为一个“事件”。现在，让我们用正式的数学符号重写公式4。设单次实验的结果为 $\omega_1$，对应的随机变量为 $X_1$。那么，所有此类可能结果的集合可以写作：

公式 5
$$S = \{\omega_1 : X_1(\omega_1) \in \mathbb{Z}^+\}$$

花括号 $\{\cdot\}$ 表示一个集合；冒号 “:” 在英文中相当于短语 “such that”（使得）；$\mathbb{Z}^+$ 表示 $X_1$ 可以取的所有非负整数值。在此上下文中，公式5可以翻译成以下自然语言陈述：

事件 $S$ 是由结果 $\omega_1$ 构成的集合，使得随机变量 $X_1$ 可以取任意非负整数值。

事件 $S$ 发生的概率是100%，因此不太有趣。通常，我们感兴趣的是 $S$ 的某个子集事件。例如，我们可能想回答这个问题：“恰好有2个人经过我们的概率是多少？” 我们可以定义另一个事件 $A$ 为我们感兴趣的那组结果；在我们的例子中，我们只对“2个人”这一结果感兴趣。

公式 6
$$A = \{2人\}$$

我们可以用更通用的数学符号将其写作：

公式 7
$$A = \{\omega_1 : X_1(\omega_1) = 2\}$$

用自然语言来说，公式7可以翻译为以下陈述：

事件 $A$ 是由结果 $\omega_1$ 构成的集合，使得随机变量 $X_1$ 取值为2。

现在我们已经理解了“事件”的概念，接下来定义概率分布函数。

概率分布函数是将事件映射到该事件发生概率的函数。

设 $P$ 为一个概率分布函数。根据定义， $P$ 是一个函数。因此， $P$ 接受一个输入并返回一个输出。该概率分布函数的输入是一个事件，而输出是某个概率值。用数学符号表示，我们可以将 $P$ 写作如下形式：

公式 8
$$P(A) \in [0, 1]$$

将公式7中事件 $A$ 的定义代入公式8，我们得到以下符号：

公式 9
$$P(\{\omega_1 : X_1(\omega_1) = 2\}) \in [0, 1]$$

这个公式看起来有些令人困惑。但使用随机变量，我们可以将公式9改写为一种更简洁、更直观的形式：

公式 10
$$P(X_1 = 2) \in [0, 1]$$

因此，使用随机变量，我们可以采用公式10所示的简洁数学符号，而不是公式1–3中冗长的自然语言描述，也避免了公式9中繁琐的数学符号。现在让我们讨论概率分布函数的类型；随着讨论的深入，随机变量的实用性将变得更加清晰。

3.1 概率质量函数

这是离散随机变量的概率分布函数。该函数接收一个随机变量的取值，并将其映射到一个概率值。例如，概率质量函数 $p_X$ 可以用以下数学符号表示：

公式 11
$$p_X(x) = P(X = x)$$

其中， $X$ 是一个离散随机变量； $x$ 是它可能取的一个样本值。根据这个定义，当 $X = x$ 时的概率质量函数值就是随机变量 $X$ 取值为 $x$ 的概率。你可以将此输出视为随机变量的“概率质量”；这类似于物理学中的质量。

公式 12
$$\text{Mass} = p_X(x)$$

如果一个随机变量只能取有限个值，或者可数无限多个值，则称其为离散随机变量。

在我们的实验例子中，我们讨论了一个随机变量 $X_1$，它表示从你身边走过的人数。理论上，这个值可能低至0（如果你身处一个安静的乡村地区），也可能高达世界人口（约80亿，如果你身处一个假想的世界级大都市）。因此，$X_1$ 可能取80亿个不同的值：1, 2, 3, …, $8 \times 10^9$ ；这是一个有限数量的值。因此， $X_1$ 是一个离散随机变量。随机变量 $X_1$ 的概率分布函数可能看起来像下面的图表。

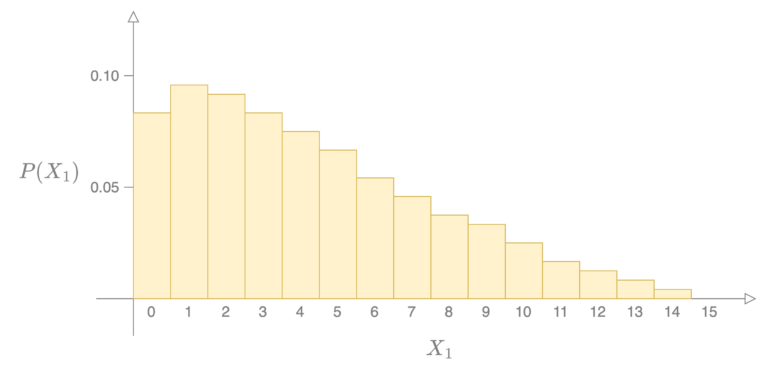图 1

横轴显示了 $X_1$ 可能取的不同整数值。纵轴显示了与 $X_1$ 对应值相关的概率。从图中可以看出，在实验中有10个人经过你的概率约为0.03。换句话说，当 $X_1 = 10$ 时的概率质量为0.03。

公式 13
$$P(X_1=10) = p_{X_1}(10) = 0.03$$

基于概率质量函数的这一定义，我们来讨论它们所具有的两个性质。

性质1：对于随机变量可以取的每一个值，概率质量函数的值都是一个大于或等于0的概率数。用数学语言，我们可以对随机变量 $X_1$ 写出如下表达式：

公式 14
$$p_{X_1}(x) \geq 0, \quad \forall x \in \mathbb{Z}^+$$

其中， $\mathbb{Z}^+$ 表示 $X_1$ 可以取的所有非负整数值。

性质2：如果我们取随机变量 $X_1$ 所有可能取的每一个值，并计算每个值处的概率质量函数值，那么总和将为1。

公式 15
$$\sum_{x} p_{X_1}(x) = 1$$

我希望离散随机变量和概率质量函数的概念现在已经清晰明了。

3.2 概率密度函数

这是连续随机变量的概率分布函数。该函数接收一个连续随机变量的取值，并将其映射到一个概率值。概率密度函数 $f_X$ 可以用以下数学符号表示：

公式 16
$$f_X(x) = \lim_{\Delta x \to 0^+} \frac{P(x - \Delta x \leq X \leq x)}{\Delta x}$$

从这个公式可以看出，概率密度函数是在连续随机变量 $X$ 取某个无穷小区间内的值时的概率（质量）除以该区间（体积）本身的长度所得的比值。因此，这里的“密度”与物理学中的密度概念相同。

公式 17
$$\text{Density} = \frac{\text{Mass}}{\text{Volume}} = f_X(x)$$

为了清晰起见，我们在公式16中需要使用极限，因为 $X$ 是一个连续随机变量，可以取实数值。该极限表示当 $\Delta x$ 从正方向趋近于0时，该密度收敛到的值。在本节中，我们将推导概率密度函数的一些性质，以便清楚地理解为何我们需要它们。但首先，让我们从连续随机变量的定义开始。

如果一个随机变量可以取不可数无限多个值，则称其为连续随机变量。

考虑随机变量 $X_3$，它表示实验中经过你的人的平均身高。这个值可能是165厘米、170厘米等。这是我们第一次尝试绘制这些数据的图表。

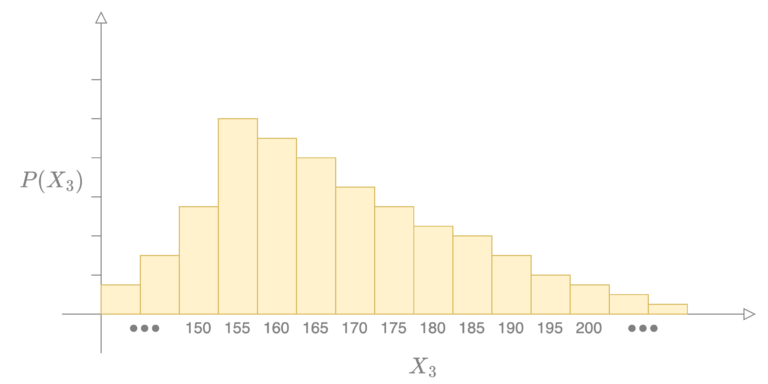图 2

这张图总体上很好地表示了数据。然而，它暗示实验中测得的平均身高只能是间隔为5的整数值。这并不一定正确；毕竟，我们可以看到平均身高可能接近166厘米的情况。因此，也许我们可以将横轴细化到每一厘米。

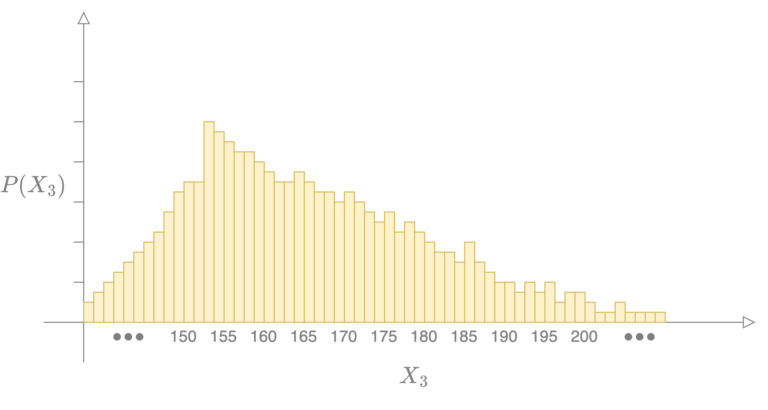图 3

但图3仍然不够准确，因为平均身高可以是165.5厘米、165.25厘米，甚至165.25495824厘米；$X_3$ 可以取的测量值有不可数无限多个。因此， $X_3$ 是一个连续随机变量。为了在图表上表示连续随机变量的分布，每个垂直矩形条的宽度需要变得无穷小；这将形成一条光滑的曲线。

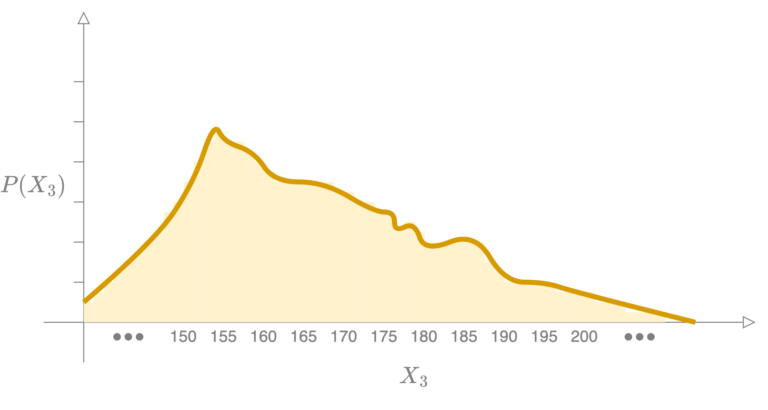图 4

性质1：连续随机变量的一个核心性质是，对于随机变量可能取的任意值，其概率质量函数的值均为0。用数学公式表示如下：

公式 18
$$p_{X3}(x) = P(X_3 = x) = 0$$

我们将通过微积分来证明这一点。让我们使用累积分布函数来证明这个事实。累积分布函数是指随机变量 $X_3$ 取小于或等于某个值 $x$ 的概率。如果我们用 $F$ 表示累积分布函数，可以写出如下符号：

公式 19
$$F_{X3}(x) = P(X_3 \leq x)$$

为了计算与连续随机变量相关的概率质量，让我们取 $X_3$ 在取值为 $x$ 和略小于 $x$ 时的累积分布函数之差。让我们仅使用概率分布函数 $P$ 的符号来观察发生了什么。

公式 20
$$P(X_3 = x) = P(X_3 \leq x) - P(X_3 \leq x - \Delta x)$$

对于连续变量， $\Delta x$ 是一个趋近于0的无穷小值。因此，我们可以用极限的数学符号表示如下：

公式 21
$$P(X_3 = x) = \lim_{\Delta x \to 0^+} [P(X_3 \leq x) - P(X_3 \leq x - \Delta x)]$$

求解这个极限，我们会发现连续随机变量 $X_3$ 在任意值 $x$ 处的概率质量函数值将为 $0$。

公式 22
$$P(X_3 = x) = [P(X_3 \leq x) - P(X_3 \leq x - \Delta x)] = 0$$

直观上，这个公式是有道理的。实验中人们的平均身高恰好为165厘米（而不是165 + $10^{-100}$ 或 165 − $10^{-100}$ ）的概率将收敛到0。这意味着在处理连续随机变量时，在某一点上实际上没有“概率质量”。因此，我们不测量质量，而是使用“密度”的概念。密度是单位体积的质量。

公式 23
$$f_{X3}(x) = \frac{\text{Mass}}{\text{Volume}} = \frac{P(X_3 \leq x) - P(X_3 \leq x - \Delta x)}{\Delta x}$$

对于像 $X_3$ 这样的连续变量，$\Delta x$ 是一个趋近于0的无穷小值。在数学上，我们用极限来表示这一点：

公式 24
$$f_{X3}(x) = \lim_{\Delta x \to 0^+} [\frac{P(X_3 \leq x) - P(X_3 \leq x - \Delta x)}{\Delta x}]$$

右边是累积分布函数导数的正式定义。

公式 25
$$f_{X3}(x) = \frac{d}{dx} [P(X_3 \leq x)]$$

性质2：由于累积分布函数的取值在0到1之间，其导数也具有类似的行为。因此，概率密度函数的另一个重要性质是它大于或等于0。

公式 26
$$f_{X3}(x) \geq 0$$

我们可以对两边积分以消除导数。

公式 27
$$\int_{-\infty}^{x} f_{X3}(x) = P(X_3 \leq x)$$

性质3：这展示了另一个重要性质：连续随机变量在其所有可能取值上的概率密度函数积分为1。

公式 28
$$\int_{-\infty}^{\infty} f_{X3}(x) = P(X_3 \leq \infty) = 1$$

若想了解更多关于概率中这些概念的小知识，请查看第6节中的配套YouTube视频链接。

3.3 联合概率分布

现在，让我们在离散和连续随机变量的背景下讨论联合概率分布。为了在机器学习/现实情境中展开有意义的讨论，让我们进行另一个实验。在 zillow.com 上随机搜索一栋房子，并记录其房价和卧室数量；对10栋房子重复此操作。现在我们定义一些随机变量：

公式 29
$$X_i: 第 i 栋房屋的卧室数量 \rightarrow \mathbb{Z}^+$$

我们定义了10个离散随机变量 $X_1$ 到 $X_{10}$，每栋房子对应一个。由于这些随机变量可以取的值是可数的，因此它们都是离散的。现在我们有了将事件结果映射为数字的随机变量，就可以进行一些分析了。例如，第一栋房子有3间卧室的概率质量可以用以下方程数学表示：

公式 30
$$p_{X1}(3) = P(X_1 = 3)$$

请记住，由于我们处理的是离散随机变量，这里指的是概率质量。同样，第三栋房子有9间卧室的概率质量可以用以下方程表示：

公式 31
$$p_{X3}(9) = P(X_3 = 9)$$

联合概率分布将表示这两个随机变量同时取某些值的概率质量。第一栋房子有3间卧室且第三栋房子有9间卧室的联合概率可以用数学方式表示如下：

公式 32
$$p_{X1,X3}(3,9) = P(X_1 = 3, X_3 = 9)$$

在这个实验中，我们观察了10栋房子；如果我们写出这10个值的联合概率，最终会得到如下符号，即从每个随机变量中采样一个值：

公式 33
$$p_{X1,X2, \dots X10}(3,7,9, \dots,4) = P(X_1 = 3, X_2 = 7, X_3 = 9, \dots, X_{10} = 4)$$

这是离散情况，概率质量函数的性质仍然成立。也就是说，概率质量大于或等于0。用数学符号表示如下：

公式 34
$$p_{X1,X2, \dots X10}(x_1, x_2, x_3, \dots, x_{10}) \geq 0$$

第二个性质指出，每个随机变量所有可能取值的联合概率质量之和应为1。

公式 35
$$\sum_{x_1} \sum_{x_2} \cdots \sum_{x_{10}} p_{X1,X2, \dots X10}(x_1, x_2, x_3, \dots, x_{10}) = 1$$

现在，让我们将例子推广到连续随机变量的情形。还记得我们在记录10栋房子时，记下了卧室数量和房价。现在我们再定义另一组10个随机变量：

公式 36
$$Y_i: 第 i 栋房屋的价格（千美元为单位） \rightarrow \mathbb{R}$$

我们定义了10个连续随机变量 $Y_1$ 到 $Y_{10}$，每栋房子对应一个。由于这些随机变量可以取的值是不可数的，因此它们都是连续的。现在我们有了将事件结果映射为数字的随机变量，就可以进行一些分析了。例如，第一栋房子价格低于30万美元的总概率密度可以用以下方程数学表示：

公式 37
$$\int_{-\infty}^{300} f_{X1}(300)\,d{x_1} = P(X_1 \leq 300)$$

同样，第三栋房子价格低于70万美元的总概率密度可以用以下方程表示：

公式 38

$$\int_{-\infty}^{700} f_{X3}(700)\,d{x_3} = P(X_3 \leq 700)$$

联合概率密度函数的性质与单个随机变量的密度函数类似。

性质1：例如，正如我们之前讨论的，连续随机变量在任意点上的概率质量为0。

公式 39

$$p_{X1,X2, \dots X10}(x_1, x_2, x_3, \dots, x_{10}) = 0$$

性质2：联合概率密度在随机变量的任意取值处都是一个大于0的数。

公式 40

$$f_{X1,X2, \dots X10}(x_1, x_2, x_3, \dots, x_{10}) \geq 0$$

性质3：此外，每个连续随机变量在其所有可能取值上的联合概率密度总和应为1。

公式 41
$$\int_{y_1} \int_{y_2} \cdots \int_{y_{10}} f_{Y_1, \dots, Y_{10}}(y_1, \dots, y_{10}) \, dy_1 \cdots dy_{10} = 1$$

在了解了概率分布的这些背景之后，现在让我们将它们与机器学习中的一个应用结合起来。

4. 机器学习应用

概率在机器学习中最基本的应用之一或许在于统计模型参数的估计。让我们继续使用在 zillow.com 上查找待售房屋信息的实验。以下是你可能会看到的一些房源列表。

图 5：来源：www.zillow.com

假设给定这些列表，我们希望建立一个统计模型，根据房屋的面积（平方英尺）、房龄和卧室数量等信息来预测房屋的售价。

图 6

在我们的 zillow.com 实验中，让我们查看10,000栋房屋，并为每栋房屋收集这些信息。最终，我们可以建立一个如下所示的表格。

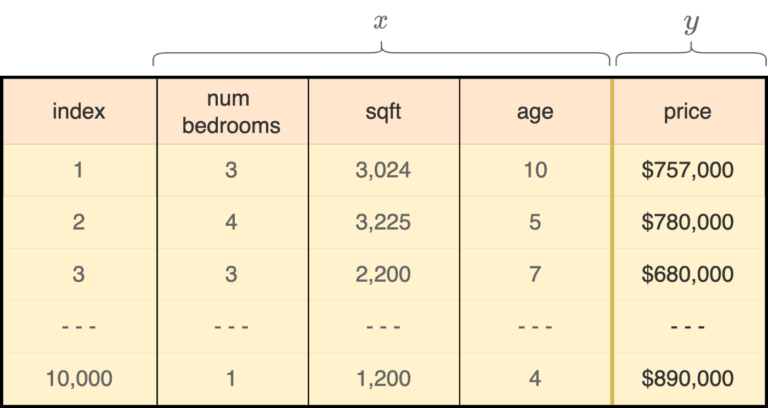图 7

现在，让我们谈谈数学是如何融入其中的。在这个实验中，我们可以将查看每栋房屋并收集信息的行为视为一个事件。因此，我们可以定义一些随机变量如下：

公式 42
$$X_i = \text{第 } i \text{ 栋房屋的卧室数量} \rightarrow \mathbb{Z}^+$$ $$W_i = \text{第 } i \text{ 栋房屋的房龄} \rightarrow \mathbb{R}$$ $$V_i = \text{第 } i \text{ 栋房屋的面积（平方英尺）} \rightarrow \mathbb{R}$$ $$Y_i = \text{第 } i \text{ 栋房屋的价格} \rightarrow \mathbb{R}$$

换句话说，对于我们在 Zillow 上看到的每栋房屋，我们可以创建4个随机变量。假设我们观察到的第5栋房屋是图5中的第一栋房屋。我们可以定义如下4个随机变量：

公式 43
$$X_5(第 5 栋房屋的卧室数量) = 3$$ $$W_5(第 5 栋房屋的房龄) = 2.5$$ $$V_5(第 5 栋房屋的面积) = 1,876$$ $$Y_5(第 5 栋房屋的价格) = 677$$

因此，对于10,000栋房屋，我们可以以相同的方式创建40,000个随机变量。于是，我们将查看 zillow.com 上房屋列表这一事件转化为了可以进行数学运算的数字。

现在我们已经定义了随机变量，那么哪些是离散随机变量，哪些是连续随机变量呢？卧室数量是可数的，因此全部10,000个 $X_i$ 随机变量都被视为离散随机变量。另一方面，房屋面积、房龄和价格都是可以取不可数无限多个值的测量值。因此，其余30,000个随机变量 $W_i$ 、 $V_i$ 、 $Y_i$ 都被视为连续随机变量。

现在，让我们利用收集到的数据和随机变量的概念来估计统计模型的参数。但在这样做之前，让我们为模型蓝图添加一些正式的数学表达。我希望这个统计模型是简单的线性回归。

公式 44
$$price= \theta_3 \times 卧室数 + \theta_2 \times 面积 + \theta_1 \times 房龄 + \theta_0 + \epsilon$$

这是线性回归的假设方程。让我们把这个方程写得更正式一些。

公式 45
$$y = \theta_3 x_i + \theta_2 v_i + \theta_1 w_i + \theta_0 + \epsilon$$

请注意，此方程中的变量 $x, y, v, w$ 并不是随机变量；它们是随机变量输出可能取的特定值。 $y$ 是我们想要预测的房价； $x, v, w$ 是我们拥有的房屋信息； $\theta$ 项是我们需要估计的模型参数； $\epsilon$ 是不可约误差。公式X中的 $\theta$ 项通常通过一种称为最大似然估计（Maximum Likelihood Estimation）的技术来计算。

4.2 最大似然估计

直观上，我们希望确定公式X中能使我们看到的10,000个房价拟合得最好的参数值；这应该是最佳模型。数学上，这等价于找到使观察到第一栋房屋价格为 $y_1$ 、第二栋房屋价格为 $y_2$ 等的联合概率密度最大的参数值。用数学符号表示如下：

公式 46
$$\hat{\theta}^{MLE} = \arg\max_{\theta} P(Y_1 = y_1, Y_2 = y_2, \dots, Y_{10000} = y_{10000} \mid \theta)$$

请注意，由于我们处理的是连续随机变量，这里使用了“密度”一词。arg max 用于表示“使该函数最大化的参数值”；该函数即联合概率密度函数。我们在机器学习中做了一个假设：房价是独立同分布（independently and identically distributed）的；我们将对此进行分解。“独立分布”意味着第一栋房屋的价格不会影响也不会被我们10,000栋房屋数据集中任何其他房屋的价格所影响；这是一个合理的假设。数学上，这意味着联合概率密度等于其各组成部分的乘积。

公式 47
$$P(Y_1 = y_1, Y_2 = y_2, \dots, Y_{10,000} = y_{10,000} \mid \theta) = \prod_{i=1}^{10,000} P(Y_i = y_i \mid \theta)$$

由于我们知道每个 $Y_i$ 都是一个连续随机变量，我们可以使用之前学到的概率密度函数符号。结果就是概率密度函数的乘积。

公式 48
$$P(Y_1 = y_1, Y_2 = y_2, \dots, Y_{10,000} = y_{10,000} \mid \theta) = \prod_{i=1}^{10,000} f_{Y_i}(y_i \mid \theta)$$

因此，我们可以将公式X的右侧替换为概率密度函数的乘积。

公式 49
$$\hat{\theta}^{MLE} = \arg\max_{\theta} \prod_{i=1}^{10,000} f_{Y_i}(y_i \mid \theta)$$

非常好！“独立同分布”中的第二部分是“同分布”。正如我们在连续随机变量部分所看到的，每个随机变量的行为可能不同；因此它们有自己的分布函数。然而，我们假设第一栋房屋潜在价格的分布与其他10,000栋房屋相同。这意味着对于任意 $Y_i$ 随机变量，在相同点处的概率密度是相同的。

公式 50
$$f_{Y_1}(600) = f_{Y_2}(600) = \cdots = f_{Y_{10,000}}(600)$$

这意味着我们可以将公式X重写为仅使用一个随机变量 $Y$，而不是10,000个 $Y_i$。

公式 51
$$\hat{\theta}^{MLE} = \arg\max_{\theta} \prod_{i=1}^{10,000} f_Y(y_i \mid \theta)$$

接下来的步骤实际上取决于我们正在构建的统计模型类型。在我们的例子中，我们试图构建一个线性回归模型；因此假设概率密度函数服从正态分布。完成这部分数学推导后的一个有趣发现是：在线性回归情况下， $\theta$ 的最优值将是使残差平方和方程最大化的值——这是机器学习中的一个基本方程。如果你对似然与概率之间联系的扩展数学讨论感兴趣，请查看我在YouTube频道“Code Emporium”上的这个视频。

5. 结论

在本文中，我们讨论了随机变量如何帮助我们量化实验结果。然后，我们借助概率分布函数理解了这些随机变量的行为。根据所测量的随机变量是离散的还是连续的，我们可以绘制不同类型的概率分布函数：离散随机变量使用概率质量函数，连续随机变量则使用概率密度函数。最后，我们通过理解如何使用最大似然估计来估计统计模型的参数，将所有这些概念与机器学习联系在一起。