循环神经网络教程（RNN）

Abid Ali Awan 2022-03-16

学习最流行的深度学习模型 RNN，并通过构建万事达卡（MasterCard）股价预测器获得动手实践经验。

什么是循环神经网络（RNN）

循环神经网络（Recurrent Neural Network，简称 RNN）是一种人工神经网络（ANN），被用于苹果的 Siri 和谷歌语音搜索等系统中。RNN 具备内部记忆机制，能够记住过去的输入信息，因此非常适合用于股票价格预测、文本生成、语音转录和机器翻译等任务。

在传统的神经网络中，输入和输出彼此独立；而在 RNN 中，输出依赖于序列中先前的元素。此外，循环网络在整个网络的每一层之间共享参数。在前馈网络中，每个节点拥有不同的权重；而 RNN 在网络的每一层内共享相同的权重，并在梯度下降过程中分别调整权重和偏置，以减少损失。

RNN

上图是循环神经网络的一个简单表示。如果我们使用简单数据 [45,56,45,49,50,…] 来预测股票价格，那么从 X₀ 到 Xₜ 的每个输入都将包含一个过去值。例如，X₀ 为 45，X₁ 为 56，这些值将用于预测序列中的下一个数字。

循环神经网络的工作原理

在 RNN 中，信息在循环中流动，因此输出由当前输入和之前接收到的输入共同决定。

输入层 X 处理初始输入并将其传递给中间层 A。中间层包含多个隐藏层，每个隐藏层都有其激活函数、权重和偏置。这些参数在隐藏层内是标准化的，因此 RNN 不会创建多个隐藏层，而是创建一个隐藏层并在时间步上循环使用。

与传统反向传播不同，循环神经网络使用随时间反向传播（Backpropagation Through Time, BPTT）算法来计算梯度。在反向传播中，模型通过从输出层到输入层计算误差来调整参数。而 BPTT 会对每个时间步的误差进行求和，因为 RNN 在各层之间共享参数。

循环神经网络的类型

前馈网络具有单一输入和输出，而循环神经网络则更加灵活，可以处理不同长度的输入和输出序列。这种灵活性使得 RNN 能够用于音乐生成、情感分类和机器翻译等任务。

根据输入和输出序列长度的不同，RNN 可分为以下四种类型：

一对一（One-to-one）：这是最简单的神经网络，常用于具有单一输入和输出的机器学习问题。
一对多（One-to-many）：具有单一输入和多个输出，常用于图像标题生成。
多对一（Many-to-one）：接收多个输入序列并预测单一输出，广泛应用于情感分类任务（输入为文本，输出为类别）。
多对多（Many-to-many）：具有多个输入和多个输出，最常见的应用是机器翻译。

RNN Types

CNN 与 RNN 的对比

卷积神经网络（Convolutional Neural Network, CNN）是一种前馈神经网络，擅长处理空间数据，常用于图像分类等计算机视觉任务。简单神经网络虽然适用于简单的二分类问题，但无法有效处理具有像素依赖关系的图像。CNN 模型架构通常包括卷积层、ReLU 层、池化层和全连接输出层。你可以通过完成《Python 中的卷积神经网络》项目来学习 CNN。

CNN Model Architecture

CNN 与 RNN 的关键区别

适用数据类型：CNN 适用于稀疏数据（如图像），而 RNN 适用于时间序列和序列数据。
训练方式：CNN 使用标准反向传播进行训练，而 RNN 使用随时间反向传播（BPTT）来计算损失。
输入/输出长度：RNN 对输入和输出长度没有限制，而 CNN 的输入和输出长度是固定的。
网络结构：CNN 是前馈网络，而 RNN 通过循环结构处理序列数据。
应用场景：CNN 主要用于视频和图像处理，而 RNN 主要用于语音和文本分析。

RNN 的局限性

简单的 RNN 模型通常会遇到两个主要问题，这些问题都与梯度（即损失函数沿误差函数的斜率）相关：

梯度消失问题（Vanishing Gradient）：当梯度变得非常小时，参数更新变得微不足道，最终导致算法停止学习。
梯度爆炸问题（Exploding Gradient）：当梯度变得过大时，模型变得不稳定。此时较大的误差梯度不断累积，导致模型权重变得过大，从而延长训练时间并降低模型性能。

解决这些问题的简单方法是减少神经网络中的隐藏层数量，从而降低 RNN 的复杂性。更有效的解决方案是使用更先进的 RNN 架构，如 LSTM 和 GRU。

RNN 的高级架构

简单的 RNN 重复模块具有基本结构，仅包含一个 tanh 层。这种简单结构存在“短期记忆”问题，即在处理较长序列数据时难以保留早期时间步的信息。这些问题可以通过长短期记忆网络（LSTM）和门控循环单元（GRU）轻松解决，因为它们能够记住长期信息。

Simple RNN Cell

长短期记忆网络（LSTM）

长短期记忆网络（Long Short-Term Memory, LSTM）是一种高级 RNN，专门设计用于防止梯度消失和梯度爆炸问题。与 RNN 类似，LSTM 也具有重复模块，但其内部结构不同。LSTM 不再使用单一的 tanh 层，而是包含四个相互作用的层。这种四层结构帮助 LSTM 保留长期记忆，可广泛应用于机器翻译、语音合成、语音识别和手写识别等序列问题。你可以通过《Python LSTM 股票预测指南》获得 LSTM 的实战经验。

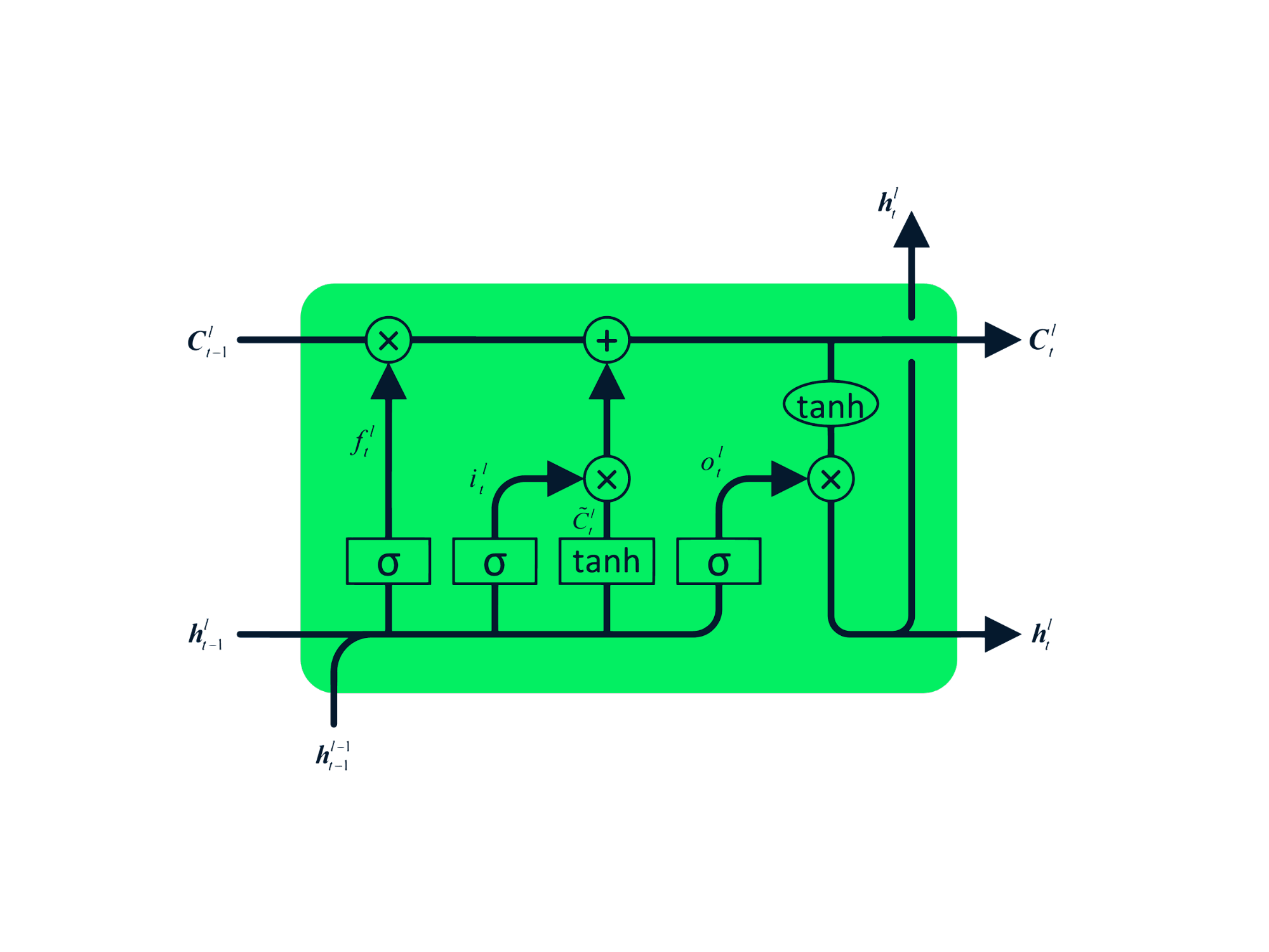
LSTM Cell

门控循环单元（GRU）

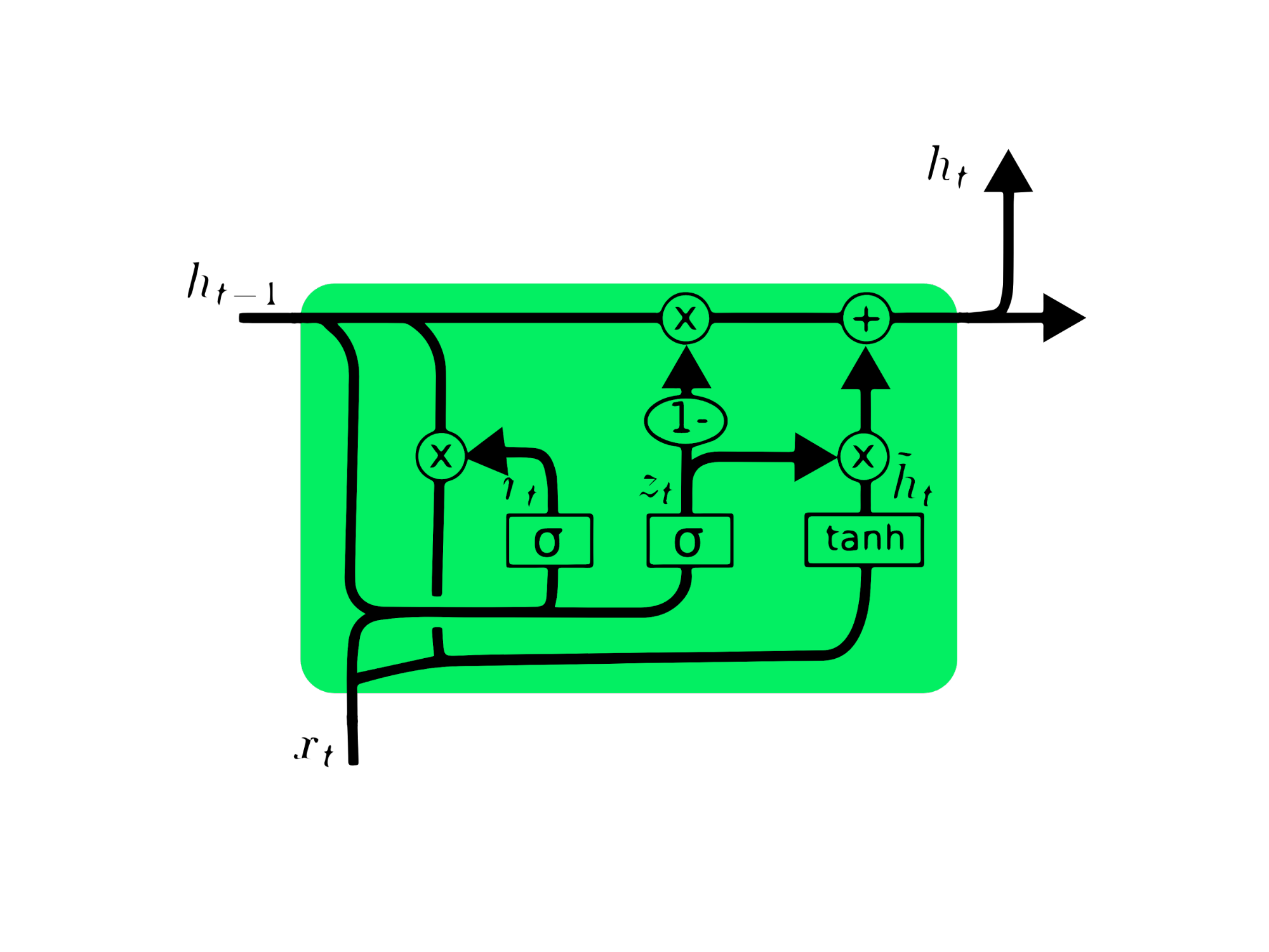
门控循环单元（Gated Recurrent Unit, GRU）是 LSTM 的一种变体，两者在设计上具有相似性，在某些情况下甚至能产生相近的结果。GRU 使用更新门（update gate）和重置门（reset gate）来解决梯度消失问题。这些门控机制可以判断哪些信息是重要的，并将其传递到输出端。这些门还可以被训练以长期存储信息，而不会随着时间推移而消失或剔除无关信息。

与 LSTM 不同，GRU 没有细胞状态（Cₜ），仅包含隐藏状态（hₜ）。由于结构更简单，GRU 的训练时间通常比 LSTM 更短。GRU 架构易于理解：它接收当前时间步的输入 xₜ 和上一时间步的隐藏状态 hₜ₋₁，并输出新的隐藏状态 hₜ。你可以在《深入理解 GRU 网络》中获取更多关于 GRU 的知识。

GRU Cell

使用 LSTM 与 GRU 预测万事达卡（MasterCard）股价

在本项目中，我们将使用 Kaggle 上的万事达卡股价数据集（时间范围：2006 年 5 月 25 日至 2021 年 10 月 11 日），训练 LSTM 和 GRU 模型以预测未来股价。这是一个基于项目的简单教程，我们将依次完成数据分析、数据预处理、在高级 RNN 模型上训练数据，并最终评估结果。

本项目需要使用 Pandas 和 NumPy 进行数据操作，Matplotlib.pyplot 进行数据可视化，scikit-learn 进行数据缩放和评估，以及 TensorFlow 进行建模。我们还将设置随机种子以确保结果可复现。

# 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout, GRU, Bidirectional
from tensorflow.keras.optimizers import SGD
from tensorflow.random import set_seed

set_seed(455)
np.random.seed(455)

数据分析

在此部分，我们将导入万事达卡数据集，将“Date”列设为索引并转换为 DateTime 格式。同时，我们会删除数据集中与股价预测无关的列，因为我们只关注股价、交易量和日期。

数据集以 Date 为索引，包含 Open（开盘价）、High（最高价）、Low（最低价）、Close（收盘价）和 Volume（交易量）等列。看起来我们已成功导入了一个清洗后的数据集。

dataset = pd.read_csv(
    "data/Mastercard_stock_history.csv", index_col="Date", parse_dates=["Date"]
).drop(["Dividends", "Stock Splits"], axis=1)
print(dataset.head())

               Open      High       Low     Close     Volume
Date                                                         
2006-05-25  3.748967  4.283869  3.739664  4.279217  395343000
2006-05-26  4.307126  4.348058  4.103398  4.179680  103044000
2006-05-30  4.183400  4.184330  3.986184  4.093164   49898000
2006-05-31  4.125723  4.219679  4.125723  4.180608   30002000
2006-06-01  4.179678  4.474572  4.176887  4.419686   62344000

使用 .describe() 函数可以深入分析数据。我们将重点关注 “High” 列，因为我们将用它来训练模型。当然，也可以选择 “Close” 或 “Open” 列作为模型特征，但 “High” 更有意义，因为它提供了当日股价达到的最高点信息。

最低股价为 4.10 美元，最高为 400.5 美元。均值为 105.9 美元，标准差为 107.3，说明股价波动较大。

print(dataset.describe())

             Open         High          Low        Close        Volume
count  3872.000000  3872.000000  3872.000000  3872.000000  3.872000e+03
mean    104.896814   105.956054   103.769349   104.882714  1.232250e+07
std     106.245511   107.303589   105.050064   106.168693  1.759665e+07
min       3.748967     4.102467     3.739664     4.083861  6.411000e+05
25%      22.347203    22.637997    22.034458    22.300391  3.529475e+06
50%      70.810079    71.375896    70.224002    70.856083  5.891750e+06
75%     147.688448   148.645373   146.822013   147.688438  1.319775e+07
max     392.653890   400.521479   389.747812   394.685730  3.953430e+08

通过 .isna().sum() 可以检查数据集中是否存在缺失值。结果显示该数据集没有缺失值。

dataset.isna().sum()

Open      0
High      0
Low       0
Close     0
Volume    0
dtype: int64

train_test_plot 函数接受三个参数：dataset、tstart 和 tend，并绘制一条简单的折线图。tstart 和 tend 是以年为单位的时间限制。我们可以更改这些参数以分析特定时间段。折线图分为两部分：训练集和测试集，这有助于我们确定测试集的分布。

自 2016 年以来，万事达卡股价持续上涨。2020 年第一季度出现下跌，但在当年下半年恢复稳定。我们的测试集包含一年的数据（2021 年至 2022 年），其余数据用于训练。

tstart = 2016
tend = 2020

def train_test_plot(dataset, tstart, tend):
    dataset.loc[f"{tstart}":f"{tend}", "High"].plot(figsize=(16, 4), legend=True)
    dataset.loc[f"{tend+1}":, "High"].plot(figsize=(16, 4), legend=True)
    plt.legend([f"Train (Before {tend+1})", f"Test ({tend+1} and beyond)"])
    plt.title("MasterCard stock price")
    plt.show()

train_test_plot(dataset,tstart,tend)

数据预处理

train_test_split 函数将数据集划分为两个子集：training_set 和 test_set。

def train_test_split(dataset, tstart, tend):
    train = dataset.loc[f"{tstart}":f"{tend}", "High"].values
    test = dataset.loc[f"{tend+1}":, "High"].values
    return train, test
training_set, test_set = train_test_split(dataset, tstart, tend)

我们将使用 MinMaxScaler 函数对训练集进行标准化，以避免异常值的影响。你也可以尝试使用 StandardScaler 或其他缩放方法来归一化数据，从而提升模型性能。

sc = MinMaxScaler(feature_range=(0, 1))
training_set = training_set.reshape(-1, 1)
training_set_scaled = sc.fit_transform(training_set)

split_sequence 函数将训练数据集转换为输入（X_train）和输出（y_train）。

例如，如果序列为 [1,2,3,4,5,6,7,8,9,10,11,12]，且 n_step 为 3，则会将其转换为三个输入时间步和一个输出，如下所示：

X	y
1,2,3	4
2,3,4	5
3,4,5	6
4,5,6	7
…	…

在本项目中，我们使用 60 个时间步（n_steps = 60）。你也可以调整该数值以优化模型性能。

def split_sequence(sequence, n_steps):
    X, y = list(), list()
    for i in range(len(sequence)):
        end_ix = i + n_steps
        if end_ix > len(sequence) - 1:
            break
        seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
        X.append(seq_x)
        y.append(seq_y)
    return np.array(X), np.array(y)

n_steps = 60
features = 1
# 转换为样本
X_train, y_train = split_sequence(training_set_scaled, n_steps)

我们处理的是单变量序列，因此特征数为 1。我们需要对 X_train 进行重塑，以适配 LSTM 模型。X_train 的原始形状为 [samples, timesteps]，我们将将其重塑为 [samples, timesteps, features]。

# 重塑 X_train 以适配模型
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], features)

LSTM 模型

该模型包含一个 LSTM 隐藏层和一个输出层。你可以尝试调整单元数量（units），更多的单元可能会带来更好的结果。在本实验中，我们将 LSTM 单元数设为 125，激活函数为 tanh，并设置输入尺寸。

作者注：TensorFlow 库非常用户友好，因此我们无需从头构建 LSTM 或 GRU 模型。只需使用 LSTM 或 GRU 模块即可轻松构建模型。

最后，我们将使用 RMSprop 优化器和均方误差（MSE）作为损失函数来编译模型。

# LSTM 架构
model_lstm = Sequential()
model_lstm.add(LSTM(units=125, activation="tanh", input_shape=(n_steps, features)))
model_lstm.add(Dense(units=1))
# 编译模型
model_lstm.compile(optimizer="RMSprop", loss="mse")

model_lstm.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm (LSTM)                  (None, 125)               63500     
_________________________________________________________________
dense (Dense)                (None, 1)                 126       
=================================================================
Total params: 63,626
Trainable params: 63,626
Non-trainable params: 0
_________________________________________________________________

模型将在 50 个 epoch 和 32 的 batch size 下进行训练。你可以调整超参数以减少训练时间或提升结果。模型训练已成功完成，并达到了最佳可能的损失值。

model_lstm.fit(X_train, y_train, epochs=50, batch_size=32)

Epoch 50/50
38/38 [==============================] - 1s 30ms/step - loss: 3.1642e-04

结果

我们将对测试集重复预处理步骤：先进行标准化，然后分割为样本，重塑后进行预测，最后将预测结果逆变换回原始尺度。

dataset_total = dataset.loc[:,"High"]
inputs = dataset_total[len(dataset_total) - len(test_set) - n_steps :].values
inputs = inputs.reshape(-1, 1)
# 标准化
inputs = sc.transform(inputs)

# 分割为样本
X_test, y_test = split_sequence(inputs, n_steps)
# 重塑
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], features)
# 预测
predicted_stock_price = model_lstm.predict(X_test)
# 逆变换
predicted_stock_price = sc.inverse_transform(predicted_stock_price)

plot_predictions 函数将绘制真实值与预测值的折线图，帮助我们直观比较两者差异。

return_rmse 函数接收测试值和预测值作为参数，并输出均方根误差（RMSE）指标。

def plot_predictions(test, predicted):
    plt.plot(test, color="gray", label="Real")
    plt.plot(predicted, color="red", label="Predicted")
    plt.title("MasterCard Stock Price Prediction")
    plt.xlabel("Time")
    plt.ylabel("MasterCard Stock Price")
    plt.legend()
    plt.show()

def return_rmse(test, predicted):
    rmse = np.sqrt(mean_squared_error(test, predicted))
    print("The root mean squared error is {:.2f}.".format(rmse))

如下图所示，单层 LSTM 模型表现良好。

plot_predictions(test_set,predicted_stock_price)

结果令人满意：模型在测试集上的 RMSE 为 6.70。

return_rmse(test_set,predicted_stock_price)
>>> The root mean squared error is 6.70.

GRU 模型

我们将保持所有设置不变，仅将 LSTM 层替换为 GRU 层，以便公平比较结果。该模型结构包含一个 125 单元的 GRU 层和一个输出层。

model_gru = Sequential()
model_gru.add(GRU(units=125, activation="tanh", input_shape=(n_steps, features)))
model_gru.add(Dense(units=1))
# 编译 RNN
model_gru.compile(optimizer="RMSprop", loss="mse")

model_gru.summary()

Model: "sequential_5"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
gru_4 (GRU)                  (None, 125)               48000     
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 126       
=================================================================
Total params: 48,126
Trainable params: 48,126
Non-trainable params: 0
_________________________________________________________________

模型已成功完成 50 个 epoch、batch size 为 32 的训练。

model_gru.fit(X_train, y_train, epochs=50, batch_size=32)

Epoch 50/50
38/38 [==============================] - 1s 29ms/step - loss: 2.6691e-04

结果

如图所示，真实值与预测值非常接近，预测曲线几乎与实际值吻合。

GRU_predicted_stock_price = model_gru.predict(X_test)
GRU_predicted_stock_price = sc.inverse_transform(GRU_predicted_stock_price)
plot_predictions(test_set, GRU_predicted_stock_price)

GRU 模型在测试集上的 RMSE 为 5.50，优于 LSTM 模型。

return_rmse(test_set,GRU_predicted_stock_price)
>>> The root mean squared error is 5.50.

结论

世界正朝着混合解决方案的方向发展，数据科学家正在图像描述生成、情绪检测、视频字幕和 DNA 测序等领域使用 CNN-RNN 混合网络。混合网络能够同时提供视觉特征和时间特征。想进一步学习 RNN，可参加课程《Python 中用于语言建模的循环神经网络》。

本教程的前半部分介绍了循环神经网络的基础知识、其局限性以及通过更高级架构（如 LSTM 和 GRU）提供的解决方案。后半部分则通过构建万事达卡股价预测器，分别使用 LSTM 和 GRU 模型进行了实践。结果清晰表明，在相同结构和超参数设置下，GRU 模型的表现优于 LSTM 模型。