Santiago Valdarrama
排序是计算机科学中研究最为深入的算法之一。存在数十种不同的排序实现和应用场景,你可以利用它们使代码更加高效和有效。
你可以使用排序来解决各种问题:
- 搜索:如果列表已排序,则在列表中查找某个项的速度要快得多。
- 选择:当数据已排序时,根据列表中其他项的关系来选择项会更容易。例如,查找第 k 大或最小的值,或者查找列表的中位数,在值按升序或降序排列时要容易得多。
- 重复项:当列表已排序时,可以非常快速地找到列表中的重复值。
- 分布:如果列表已排序,则分析列表中各项的频率分布会非常快。例如,找出出现最频繁或最不频繁的元素在已排序列表中相对简单。
从商业应用到学术研究,以及介于两者之间的各种场景,你都可以通过排序节省大量时间和精力。
Python 的内置排序算法
Python 语言(像许多其他高级编程语言一样)提供了开箱即用的数据排序功能,可通过 sorted() 实现。以下是对整数数组进行排序的示例:
>>> array = [8, 2, 6, 4, 5]
>>> sorted(array)
[2, 4, 5, 6, 8]
只要列表内的值可比较,你就可以使用 sorted() 对任何列表进行排序。
时间复杂度的重要性
本教程涵盖两种衡量排序算法运行时间的方法:
- 实践角度:你将使用
timeit模块测量实现的实际运行时间。 - 理论角度:你将使用大 O 表示法(Big O notation)衡量算法的运行时间复杂度。
为你的代码计时
在比较 Python 中的两种排序算法时,查看每种算法的运行时间总是很有参考价值的。每次算法所花费的具体时间部分取决于你的硬件,但你仍可使用执行时间之间的比例来判断哪种实现更高效。
在本节中,你将重点学习一种实用方法:使用 timeit 模块实际测量排序算法的运行时间。有关在 Python 中为代码执行计时的不同方法的更多信息,请参阅《Python 计时器函数:三种监控代码的方式》。
以下是一个可用于为算法计时的函数:
from random import randint
from timeit import repeat
def run_sorting_algorithm(algorithm, array):
# 设置上下文并准备调用指定算法(使用提供的数组)
# 如果不是内置的 `sorted()`,则导入算法函数
setup_code = f"from __main__ import {algorithm}" \
if algorithm != "sorted" else ""
stmt = f"{algorithm}({array})"
# 执行代码十次,并返回每次执行所花费的时间(秒)
times = repeat(setup=setup_code, stmt=stmt, repeat=3, number=10)
# 最后,显示算法名称及其最短运行时间
print(f"Algorithm: {algorithm}. Minimum execution time: {min(times)}")
在此示例中,run_sorting_algorithm() 接收算法名称和需要排序的输入数组。以下是逐行解释其工作原理:
- 第 8 行使用 Python f-string 的特性导入算法名称,以便
timeit.repeat()知道从何处调用该算法。注意:这仅对本教程中使用的自定义实现是必要的;如果指定的是内置sorted(),则无需导入。 - 第 11 行使用提供的数组准备对算法的调用。这是将被执行和计时的语句。
- 第 15 行使用 setup 代码和语句调用
timeit.repeat()。这将调用指定的排序算法十次,并返回每次执行所花费的秒数。 - 第 19 行找出返回的最短时间,并将其与算法名称一起打印。
注意:一个常见的误解是应取每次运行的平均时间,而非选择最短时间。由于系统同时运行其他进程,时间测量具有噪声。最短时间始终是最少噪声的,因此最能代表算法的真实运行时间。
以下是如何使用 run_sorting_algorithm() 来确定使用 sorted() 对一万个整数值数组进行排序所需时间的示例:
ARRAY_LENGTH = 10000
if __name__ == "__main__":
# 生成一个包含 `ARRAY_LENGTH` 个随机整数(0 到 999 之间)的数组
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
# 使用排序算法名称和刚创建的数组调用函数
run_sorting_algorithm(algorithm="sorted", array=array)
如果你将上述代码保存为 sorting.py 文件,则可以从终端运行并查看输出:
$ python sorting.py
Algorithm: sorted. Minimum execution time: 0.010945824000000007
请记住,每次实验的秒数部分取决于你使用的硬件,因此运行代码时可能会看到略有不同的结果。
注意:你可以在 Python 官方文档 中了解更多关于
timeit模块的信息。
使用大 O 表示法衡量效率
仅凭算法运行的具体时间不足以全面了解其时间复杂度。为解决此问题,你可以使用大 O 表示法(Big O notation)。大 O 常用于比较不同实现并决定哪种最高效,它忽略不必要的细节,专注于算法运行时间中最关键的部分。
不同算法所需的运行时间可能受若干无关因素影响,包括处理器速度或可用内存。而大 O 提供了一种与硬件无关的方式来表达运行时间复杂度。使用大 O,你可以根据算法运行时间相对于输入规模的增长速度来表达其复杂度,尤其是在输入规模变得极大时。
假设 是算法输入的大小,则大 O 表示法表示 与算法为找到解决方案所需步骤数之间的关系。大 O 使用大写字母 “O” 后跟括号内的这种关系。例如, 表示执行步骤数与输入大小成正比的算法。
尽管本教程不会深入探讨大 O 表示法的细节,以下是五种不同算法运行时间复杂度的示例:
| 大 O 复杂度 | 描述 |
|---|---|
| 常数时间:无论输入大小如何,运行时间恒定。例如,在哈希表中查找元素。 | |
| 线性时间:运行时间随输入大小线性增长。例如,检查列表中每个项是否满足某个条件。 | |
| 平方时间:运行时间是输入大小的二次函数。例如,一种朴素的查找列表中重复值的实现(需对每个项检查两次)。 | |
| 指数时间:运行时间随输入大小呈指数增长。这类算法被认为极其低效。例如,三着色问题。 | |
| 对数时间:当输入大小呈指数增长时,运行时间线性增长。例如,处理一千个元素需 1 秒,则处理一万需 2 秒,十万需 3 秒,依此类推。二分查找即为对数时间算法的示例。 |
本教程涵盖了所讨论的每种排序算法的大 O 运行时间复杂度,并简要解释了如何确定每种情况下的运行时间。这将帮助你更好地理解如何开始使用大 O 对其他算法进行分类。
Python 中的冒泡排序算法
冒泡排序是最直观的排序算法之一。其名称源于算法的工作方式:在每次新遍历中,列表中的最大元素会“冒泡”到其正确位置。
冒泡排序通过多次遍历列表,逐一比较相邻元素,并交换顺序错误的相邻项。
在 Python 中实现冒泡排序
以下是 Python 中冒泡排序算法的实现:
def bubble_sort(array):
n = len(array)
for i in range(n):
# 创建一个标志,若已无内容可排序,则提前终止
already_sorted = True
# 逐个查看列表中的每个项,
# 并与其相邻值比较。
# 随着每次迭代,待查看的数组部分会缩小,
# 因为剩余项已被排序。
for j in range(n - i - 1):
if array[j] > array[j + 1]:
# 若当前项大于其相邻值,则交换它们
array[j], array[j + 1] = array[j + 1], array[j]
# 由于交换了两个元素,
# 将 `already_sorted` 标志设为 `False`
# 以防止算法过早结束
already_sorted = False
# 若在最后一次迭代中未发生交换,
# 则数组已排序,可终止
if already_sorted:
break
return array
由于此实现在升序中对数组排序,因此每一步都会将最大元素“冒泡”到数组末尾。这意味着每次迭代所需的步骤都比前一次少,因为数组的连续更大一部分已被排序。
第 4 行和第 10 行的循环决定了算法遍历列表的方式。注意 j 最初从列表的第一个元素运行到倒数第二个元素。在第二次迭代中,j 运行到倒数第三个元素,依此类推。在每次迭代结束时,列表的末尾部分将被排序。
随着循环进行,第 15 行将每个元素与其相邻值进行比较,第 18 行在顺序错误时交换它们。这确保了函数结束时列表已排序。
注意:上述代码第 13、23 和 27 行的
already_sorted标志是对算法的一种优化,并非完整冒泡排序实现所必需。但它允许函数在列表完全排序后跳过不必要的步骤。
作为练习,你可以移除该标志的使用,并比较两种实现的运行时间。
为正确分析算法的工作原理,考虑一个值为 [8, 2, 6, 4, 5] 的列表。假设你使用上述 bubble_sort()。下图展示了算法进行过程中数组在每次迭代时的状态:
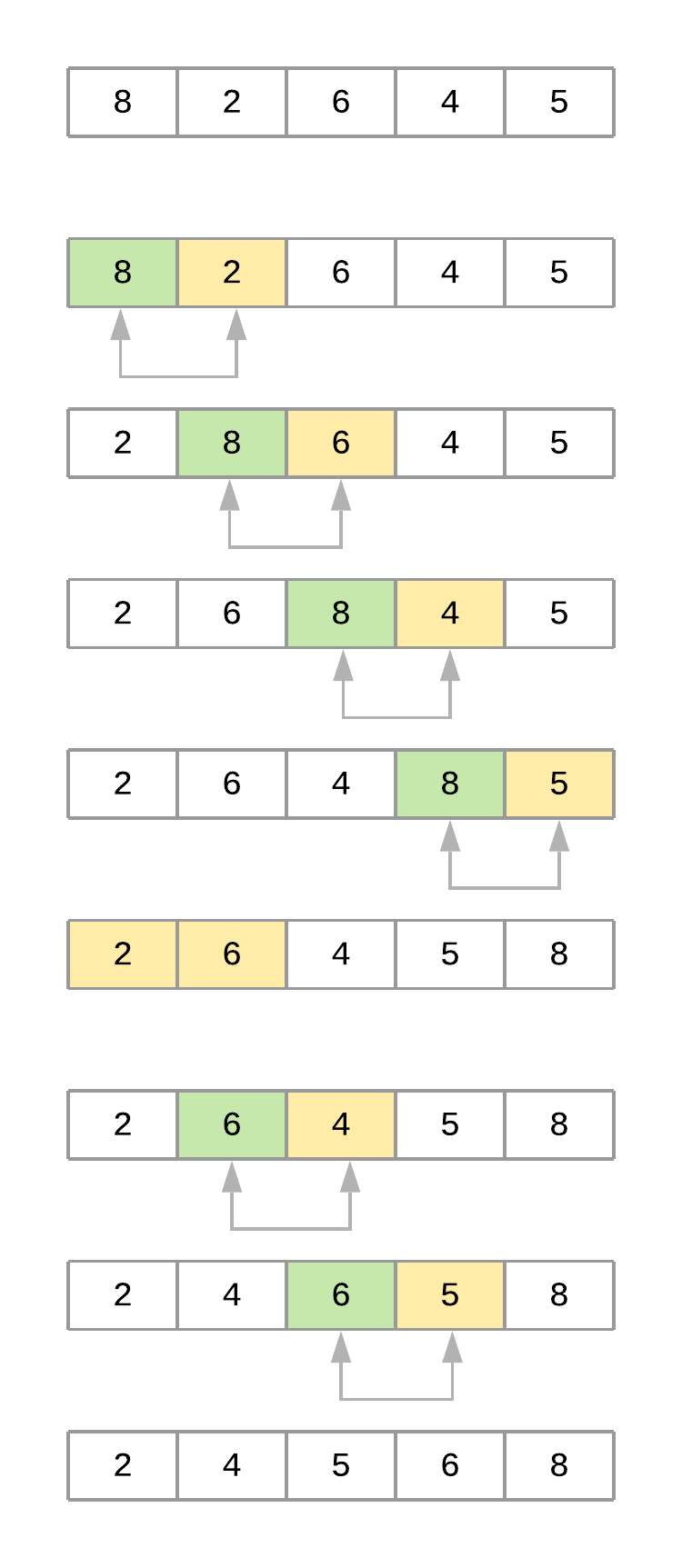
冒泡排序过程
现在逐步查看算法进行时数组的变化:
- 代码首先比较第一个元素 8 与其相邻元素 2。由于 8 > 2,值被交换,结果为:
[2, 8, 6, 4, 5]。 - 然后算法比较第二个元素 8 与其相邻元素 6。由于 8 > 6,值被交换,结果为:
[2, 6, 8, 4, 5]。 - 接着,算法比较第三个元素 8 与其相邻元素 4。由于 8 > 4,值也被交换,结果为:
[2, 6, 4, 8, 5]。 - 最后,算法比较第四个元素 8 与其相邻元素 5,并交换它们,结果为
[2, 6, 4, 5, 8]。此时,算法完成了第一轮遍历(i = 0)。注意值 8 已从初始位置“冒泡”到列表末尾的正确位置。 - 第二轮(
i = 1)考虑到列表最后一个元素已就位,专注于剩余四个元素[2, 6, 4, 5]。在此轮结束时,值 6 找到了其正确位置。第三轮将值 5 定位,依此类推,直到列表排序完成。
冒泡排序的大 O 运行时间复杂度分析
你的冒泡排序实现包含两个嵌套的 for 循环,算法执行 次比较,然后 次,依此类推,直到最后一次比较。总比较次数为 ,也可写作 。
如前所述,大 O 关注运行时间相对于输入大小的增长情况。因此,要将上述公式转换为算法的大 O 复杂度,你需要去除常数项(因为它们不随输入大小变化)。
这样做可简化为 。由于 的增长速度远快于 ,因此可忽略最后一项,最终冒泡排序的平均和最坏情况复杂度为 。
在算法接收到已排序数组的情况下(且实现包含前述 already_sorted 标志优化),运行时间复杂度将降至更好的 ,因为算法无需多次访问任何元素。
因此, 是冒泡排序的最佳情况运行时间复杂度。但请记住,最佳情况属于例外,比较不同算法时应关注平均情况。
冒泡排序实现的计时
使用前面介绍的 run_sorting_algorithm(),以下是冒泡排序处理一万个元素数组所需的时间。第 8 行替换了算法名称,其余保持不变:
if __name__ == "__main__":
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
run_sorting_algorithm(algorithm="bubble_sort", array=array)
现在运行脚本以获取 bubble_sort 的执行时间:
$ python sorting.py
Algorithm: bubble_sort. Minimum execution time: 73.21720498399998
对一万个元素的数组排序耗时 73 秒。这是 run_sorting_algorithm() 运行十次中最快的执行时间。多次执行此脚本将产生类似结果。
注意:单次冒泡排序执行耗时 73 秒,但算法使用
timeit.repeat()运行了十次。这意味着在类似硬件条件下,你的代码预计需要约 73 × 10 = 730 秒才能运行完毕。较慢的机器可能需要更长时间。
冒泡排序的优缺点分析
冒泡排序算法的主要优点是简单。它既易于实现又易于理解。这可能是大多数计算机科学课程在介绍排序主题时首选冒泡排序的主要原因。
如前所述,冒泡排序的缺点是速度慢,其运行时间复杂度为 。不幸的是,这使其无法成为对大型数组进行排序的实用候选方案。
Python 中的插入排序算法
与冒泡排序类似,插入排序算法也易于实现和理解。但与冒泡排序不同,它通过逐个比较每个项与列表其余部分并将该项插入正确位置,从而逐步构建已排序列表。这种“插入”过程赋予了该算法其名称。
解释插入排序的一个绝佳类比是你整理一副扑克牌的方式。想象你手中握有一组卡片,希望将它们排序。你会从一张卡片开始,逐步将其与其余卡片比较,直到找到其正确位置。此时,你将卡片插入正确位置,并对新卡片重复此过程,直到手中所有卡片排序完毕。
在 Python 中实现插入排序
插入排序算法的工作方式与上述扑克牌示例完全相同。以下是 Python 中的实现:
def insertion_sort(array):
# 从数组的第二个元素循环到最后一个元素
for i in range(1, len(array)):
# 这是我们希望在其正确位置定位的元素
key_item = array[i]
# 初始化一个变量,用于
# 找到 `key_item` 引用元素的正确位置
j = i - 1
# 遍历左侧部分的列表项,
# 仅在 `key_item` 小于其相邻值时
# 找到其正确位置
while j >= 0 and array[j] > key_item:
# 将值向左移动一位
# 并重新定位 j 以指向下一个元素(从右到左)
array[j + 1] = array[j]
j -= 1
# 完成元素移动后,
# 可将 `key_item` 放置在其正确位置
array[j + 1] = key_item
return array
与冒泡排序不同,此插入排序实现在左侧推动较小项以构建已排序列表。以下是逐行解析 insertion_sort():
- 第 4 行设置了循环,确定函数在每次迭代中要定位的
key_item。注意循环从列表的第二个项开始,一直到最后一项。 - 第 7 行使用函数试图放置的项初始化
key_item。 - 第 12 行初始化一个变量,该变量将依次指向
key_item左侧的每个元素。这些是要与key_item依次比较的元素。 - 第 18 行使用 while 循环将
key_item与其左侧的每个值进行比较,并移动元素以为key_item腾出空间。 - 第 27 行在算法将所有较大值向右移动后,将
key_item放置在其正确位置。
下图展示了对数组 [8, 2, 6, 4, 5] 进行排序时算法的不同迭代:
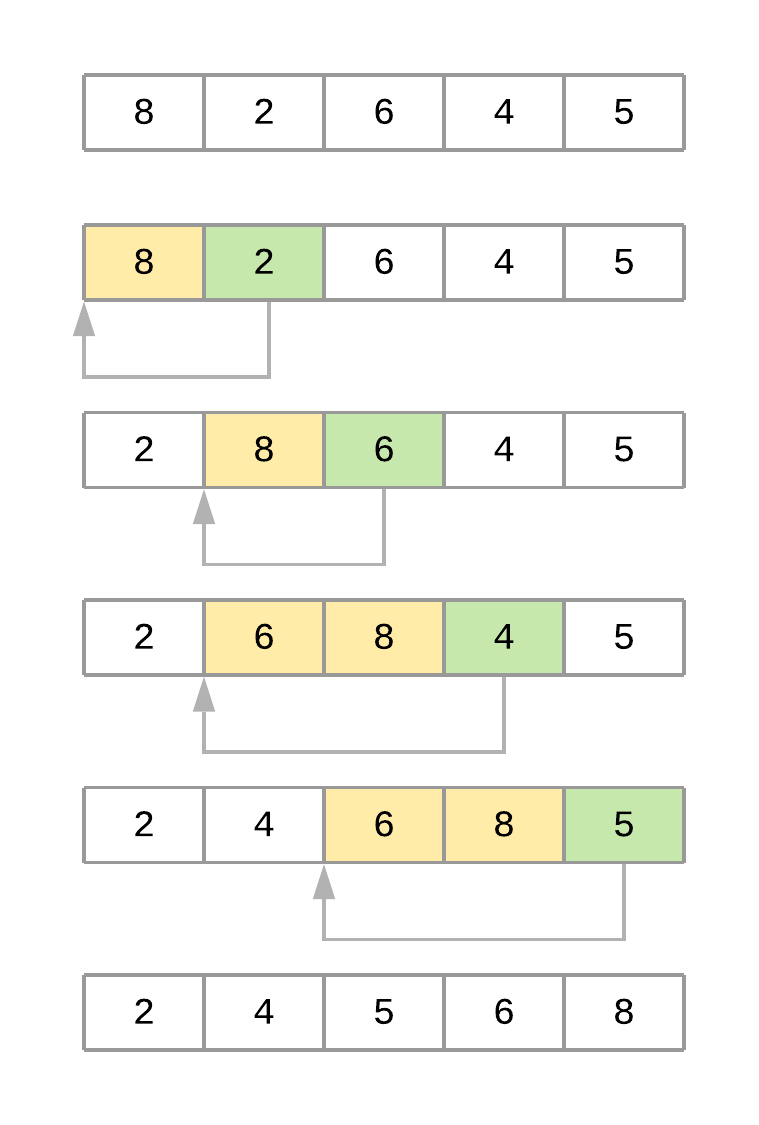
插入排序过程
以下是算法对数组排序时的步骤摘要:
- 算法从
key_item = 2开始,遍历其左侧的子数组以找到其正确位置。此时子数组为[8]。 - 由于 2 < 8,算法将元素 8 向右移动一位。此时数组为
[8, 8, 6, 4, 5]。 - 由于子数组中没有更多元素,
key_item现在被放置在其新位置,最终数组为[2, 8, 6, 4, 5]。 - 第二轮从
key_item = 6开始,遍历其左侧的子数组[2, 8]。 - 由于 6 < 8,算法将 8 向右移动。此时数组为
[2, 8, 8, 4, 5]。 - 由于 6 > 2,算法无需继续遍历子数组,因此定位
key_item并完成第二轮。此时数组为[2, 6, 8, 4, 5]。 - 第三轮将元素 4 放置到正确位置,第四轮将元素 5 放置到位,最终数组排序完成。
插入排序的大 O 运行时间复杂度分析
与冒泡排序实现类似,插入排序算法也有几个嵌套循环遍历列表。内层循环相当高效,因为它只遍历到找到元素的正确位置为止。尽管如此,该算法在平均情况下的运行时间复杂度仍为 。
最坏情况发生在提供的数组按逆序排序时。此时,内层循环必须执行每次比较以将每个元素放置到正确位置。这仍然给出 的运行时间复杂度。
最佳情况发生在提供的数组已排序时。此时,内层循环从不执行,导致 的运行时间复杂度,与冒泡排序的最佳情况相同。
尽管冒泡排序和插入排序具有相同的大 O 运行时间复杂度,但在实践中,插入排序明显比冒泡排序更高效。如果你查看两种算法的实现,就会发现插入排序为排序列表所需的比较次数更少。
插入排序实现的计时
为证明插入排序比冒泡排序更高效的断言,你可以为插入排序算法计时并与冒泡排序的结果进行比较。为此,只需将 run_sorting_algorithm() 调用替换为插入排序实现的名称:
if __name__ == "__main__":
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
run_sorting_algorithm(algorithm="insertion_sort", array=array)
你可以像之前一样执行脚本:
$ python sorting.py
Algorithm: insertion_sort. Minimum execution time: 56.71029764299999
注意插入排序实现比冒泡排序实现对同一数组排序少用了约 17 秒。尽管两者都是 算法,但插入排序更高效。
插入排序的优缺点分析
与冒泡排序一样,插入排序算法的实现也非常简单。尽管插入排序是 算法,但在实践中它比冒泡排序等其他二次实现要高效得多。
存在更强大的算法,包括归并排序和快速排序,但这些实现是递归的,通常在处理小型列表时无法击败插入排序。某些快速排序实现甚至在列表足够小时内部使用插入排序,以提供更快的整体实现。Timsort 也使用插入排序在内部对输入数组的小部分进行排序。
尽管如此,插入排序对于大型数组并不实用,这为能够以更高效方式扩展的算法打开了大门。
Python 中的归并排序算法
归并排序是一种非常高效的排序算法。它基于分治法(divide-and-conquer)——一种用于解决复杂问题的强大算法技术。
要正确理解分治法,你首先应理解递归的概念。递归涉及将问题分解为更小的子问题,直到它们足够小以便管理。在编程中,递归通常通过函数调用自身来表达。
分治算法通常遵循相同的结构:
- 将原始输入分解为若干部分,每部分代表一个与原始问题相似但更简单的子问题。
- 递归地解决每个子问题。
- 将所有子问题的解组合成一个整体解。
在归并排序的情况下,分治法将输入值集分为两个等大的部分,递归地对每半部分排序,最后将这两个已排序的部分合并为一个已排序的列表。
在 Python 中实现归并排序
归并排序算法的实现需要两个不同的部分:
- 一个递归地将输入分成两半的函数
- 一个合并两半并生成已排序数组的函数
以下是合并两个不同数组的代码:
def merge(left, right):
# 如果第一个数组为空,则无需合并,
# 直接返回第二个数组作为结果
if len(left) == 0:
return right
# 如果第二个数组为空,则无需合并,
# 直接返回第一个数组作为结果
if len(right) == 0:
return left
result = []
index_left = index_right = 0
# 现在遍历两个数组,直到所有元素
# 都进入结果数组
while len(result) < len(left) + len(right):
# 需要对元素进行排序才能将其添加到
# 结果数组中,因此需要决定
# 从第一个还是第二个数组获取下一个元素
if left[index_left] <= right[index_right]:
result.append(left[index_left])
index_left += 1
else:
result.append(right[index_right])
index_right += 1
# 如果到达任一数组的末尾,
# 则可将另一个数组的剩余元素
# 添加到结果中并跳出循环
if index_right == len(right):
result += left[index_left:]
break
if index_left == len(left):
result += right[index_right:]
break
return result
merge() 接收两个需要合并的不同已排序数组。完成此操作的过程很简单:
- 第 4 行和第 9 行检查任一数组是否为空。如果其中一个为空,则无需合并,函数返回另一个数组。
- 第 17 行启动一个 while 循环,当结果包含来自两个提供数组的所有元素时结束。目标是查看两个数组并组合其项以生成已排序列表。
- 第 21 行比较两个数组头部的元素,选择较小的值并将其附加到结果数组的末尾。
- 第 31 行和第 35 行在任一数组的所有元素都已使用时,将剩余元素附加到结果中。
有了上述函数,唯一缺少的部分是一个递归地将输入数组分成两半并使用 merge() 生成最终结果的函数:
def merge_sort(array):
# 如果输入数组包含少于两个元素,
# 则将其作为函数结果返回
if len(array) < 2:
return array
midpoint = len(array) // 2
# 通过递归地将输入分成两个相等的半部分、
# 对每半部分排序并将它们合并到最终结果中来对数组排序
return merge(
left=merge_sort(array[:midpoint]),
right=merge_sort(array[midpoint:])
)
以下是代码的快速摘要:
- 第 44 行充当递归的停止条件。如果输入数组包含少于两个元素,则函数返回该数组。注意,此条件可能由接收单个项或空数组触发。在这两种情况下,都无需排序,因此函数应返回。
- 第 47 行计算数组的中点。
- 第 52 行调用
merge(),传入两个已排序的半部分作为数组。
注意此函数如何递归地调用自身,每次将数组减半。每次迭代处理一个不断缩小的数组,直到剩余元素少于两个,意味着无需再排序。此时,merge() 接管,合并两个半部分并生成已排序列表。
下图展示了归并排序对数组 [8, 2, 6, 4, 5] 进行排序的步骤:
归并排序过程
图中黄色箭头表示在每个递归级别将数组减半。绿色箭头表示将每个子数组合并回一起。步骤可总结如下:
- 对
[8, 2, 6, 4, 5]的第一次merge_sort()调用将中点定义为 2。中点用于将输入数组分为array[:2]和array[2:],分别生成[8, 2]和[6, 4, 5]。然后对每半部分递归调用merge_sort()以分别排序。 - 对
[8, 2]的merge_sort()调用生成[8]和[2]。对这些半部分重复此过程。 - 对
[8]的merge_sort()调用返回[8],因为这是唯一元素。对[2]的调用同理。 - 此时,函数开始使用
merge()将子数组合并回一起,以[8]和[2]作为输入数组,生成[2, 8]作为结果。 - 另一方面,
[6, 4, 5]使用相同过程递归分解和合并,生成[4, 5, 6]作为结果。 - 在最后一步,
[2, 8]和[4, 5, 6]使用merge()合并回一起,生成最终结果:[2, 4, 5, 6, 8]。
归并排序的大 O 复杂度分析
要分析归并排序的复杂度,你可以分别查看其两个步骤:
merge()具有线性运行时间。它接收两个数组,其组合长度最多为 n$(原始输入数组的长度),并通过最多查看每个元素一次来合并两个数组。这导致运行时间复杂度为 $O(n)。- 第二步递归地将输入数组拆分,并为每半部分调用
merge()。由于数组被拆分直到只剩单个元素,此函数执行的拆分操作总数为 。由于merge()为每半部分调用,我们得到总运行时间为 。
有趣的是, 是排序算法所能达到的最佳可能最坏情况运行时间。
归并排序实现的计时
要将归并排序的速度与前两种实现进行比较,你可以使用与之前相同的机制,只需在第 8 行替换算法名称:
if __name__ == "__main__":
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
run_sorting_algorithm(algorithm="merge_sort", array=array)
你可以执行脚本以获取 merge_sort 的执行时间:
$ python sorting.py
Algorithm: merge_sort. Minimum execution time: 0.6195857160000173
与冒泡排序和插入排序相比,归并排序实现在不到一秒内对一万个元素的数组进行了排序!
归并排序的优缺点分析
得益于其 的运行时间复杂度,归并排序是一种非常高效的算法,随着输入数组大小的增长而良好扩展。它也易于并行化,因为它将输入数组分解为可并行分发和处理的块(如有必要)。
尽管如此,对于小型列表,递归的时间成本使得冒泡排序和插入排序等算法更快。例如,对十个元素的列表进行实验得到以下时间:
Algorithm: bubble_sort. Minimum execution time: 0.000018774999999998654
Algorithm: insertion_sort. Minimum execution time: 0.000029786000000000395
Algorithm: merge_sort. Minimum execution time: 0.00016983000000000276
冒泡排序和插入排序在对十个元素的列表排序时都击败了归并排序。
归并排序的另一个缺点是它在递归调用自身时创建了数组的副本。它还在 merge() 内部创建了一个新列表来排序并返回两个输入半部分。这使得归并排序比冒泡排序和插入排序使用更多内存,后两者都能就地排序列表。
由于此限制,在内存受限的硬件上对大型列表排序时,你可能不想使用归并排序。
Python 中的快速排序算法
与归并排序一样,快速排序算法也应用分治原则将输入数组分为两个列表:一个包含较小项,另一个包含较大项。然后算法递归地对两个列表排序,直到整个列表完全排序。
将输入列表划分为两部分称为分区(partitioning)。快速排序首先选择一个基准(pivot)元素,并围绕基准对列表进行分区,将每个较小元素放入低数组,每个较大元素放入高数组。
将低列表中的每个元素放在基准左侧,高列表中的每个元素放在基准右侧,这恰好将基准定位在最终已排序列表中所需的位置。这意味着函数现在可以递归地对低列表和高列表应用相同过程,直到整个列表排序完成。
在 Python 中实现快速排序
以下是快速排序的紧凑实现:
from random import randint
def quicksort(array):
# 如果输入数组包含少于两个元素,
# 则将其作为函数结果返回
if len(array) < 2:
return array
low, same, high = [], [], []
# 随机选择 `pivot` 元素
pivot = array[randint(0, len(array) - 1)]
for item in array:
# 小于 `pivot` 的元素进入 `low` 列表。
# 大于 `pivot` 的元素进入 `high` 列表。
# 等于 `pivot` 的元素进入 `same` 列表。
if item < pivot:
low.append(item)
elif item == pivot:
same.append(item)
elif item > pivot:
high.append(item)
# 最终结果结合了已排序的 `low` 列表、
# `same` 列表和已排序的 `high` 列表
return quicksort(low) + same + quicksort(high)
以下是代码摘要:
- 第 6 行在数组包含少于两个元素时停止递归函数。
- 第 12 行从列表中随机选择基准元素并继续对列表进行分区。
- 第 19-20 行将每个小于
pivot的元素放入名为low的列表。 - 第 21-22 行将每个等于
pivot的元素放入名为same的列表。 - 第 23-24 行将每个大于
pivot的元素放入名为high的列表。 - 第 28 行递归地对
low和high列表排序,并将它们与same列表的内容组合在一起。
下图展示了快速排序对数组 [8, 2, 6, 4, 5] 进行排序的步骤:
快速排序过程
黄色线条表示将数组划分为三个列表:low、same 和 high。绿色线条表示对这些列表进行排序并重新组合。以下是步骤的简要说明:
- 基准元素被随机选择。在此情况下,
pivot为 6。 - 第一次遍历将输入数组分区,使
low包含[2, 4, 5],same包含[6],high包含[8]。 - 然后对
low递归调用quicksort()。这会随机选择一个基准并将数组分解为[2](low)、[4](same)和[5](high)。 - 该过程继续,但此时
low和high都包含少于两个项。这结束了递归,函数将数组重新组合。将已排序的low和high添加到same列表的两侧生成[2, 4, 5]。 - 另一方面,包含
[8]的high列表包含少于两个元素,因此算法返回已排序的low数组(现在为[2, 4, 5])。将其与same([6])和high([8])合并生成最终已排序列表。
选择基准元素
为什么上述实现随机选择基准元素?始终选择输入列表的第一个或最后一个元素不是一样的吗?
由于快速排序算法的工作方式,递归级别的数量取决于每次分区中基准的最终位置。在最佳情况下,算法始终选择中位数作为基准。这将使每个生成的子问题恰好是前一个问题大小的一半,最多导致 个级别。
另一方面,如果算法始终选择数组的最小或最大元素作为基准,则生成的分区将尽可能不均等,导致 个递归级别。这将是快速排序的最坏情况。
如你所见,快速排序的效率通常取决于基准的选择。如果输入数组未排序,则使用第一个或最后一个元素作为基准与使用随机元素效果相同。但如果输入数组已排序或几乎已排序,使用第一个或最后一个元素作为基准可能导致最坏情况。随机选择基准更可能使快速排序选择接近中位数的值并更快完成。
选择基准的另一种选项是找到数组的中位数值并强制算法将其用作基准。这可以在 时间内完成。尽管该过程稍微复杂一些,但使用中位数作为快速排序的基准可保证你获得最佳情况的大 O 场景。
快速排序(Quicksort)的时间复杂度分析
在快速排序中,输入列表的划分操作可以在 线性时间 O(n) 内完成,并且该过程平均会递归执行 log₂n 次。因此,其总体时间复杂度为 O(n log₂n)。
不过,请记住我们之前讨论过:枢轴(pivot)的选择会影响算法的运行时间。
- 最佳情况 O(n log n) 出现在所选枢轴接近数组中位数时;
- 最坏情况 O(n²) 则发生在每次选择的枢轴都是数组中的最小值或最大值时。
理论上,如果算法首先找出数组的中位数并将其用作枢轴,那么最坏情况下的时间复杂度也能降至 O(n log₂n)。因为可以在 线性时间 O(n) 内找到中位数,而使用中位数作为枢轴可以保证快速排序部分始终以 O(n log₂n) 运行。
这样一来,总运行时间为 O(n) + O(n log₂n)。由于对数项增长速度远快于线性项,我们可以简化为 O(n log₂n)。
注意:虽然理论上可以通过选择中位数作为枢轴将快速排序的最坏情况优化到 O(n log₂n),但在实践中很少采用这种方法。只有当待排序列表非常大时,这种实现才可能比简单的随机选择枢轴更快。
随机选择枢轴 可以使最坏情况变得极不可能发生。因此,对于大多数实际应用而言,随机枢轴已经足够优秀。
对你的快速排序实现进行计时
你现在应该已经熟悉了对算法运行时间进行计时的方法。只需修改第 8 行中的算法名称即可:
if __name__ == "__main__":
# 生成一个包含 `ARRAY_LENGTH` 个元素的数组,
# 元素为 0 到 999 之间的随机整数
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
# 调用函数,传入排序算法名称和刚创建的数组
run_sorting_algorithm(algorithm="quicksort", array=array)
像之前一样运行脚本:
$ python sorting.py
Algorithm: quicksort. Minimum execution time: 0.11675417600002902
不仅快速排序在不到一秒内完成,而且它比归并排序快得多(0.11 秒 vs 0.61 秒)。
如果将 ARRAY_LENGTH 从 10,000 增加到 1,000,000 并再次运行脚本,归并排序需要 97 秒,而快速排序仅需 10 秒!
快速排序的优缺点分析
正如其名,快速排序确实非常快。尽管其理论最坏情况是 O(n²),但在实践中,一个良好的快速排序实现在大多数情况下都优于其他排序算法。此外,与归并排序一样,快速排序也易于并行化。
然而,快速排序的主要缺点是无法保证达到平均时间复杂度。虽然最坏情况很少出现,但某些对性能稳定性要求极高的应用场景无法承担这种风险,因此会选择那些无论输入如何都能稳定保持 O(n log₂n) 的算法。
与归并排序类似,快速排序也以空间换速度。这在处理大规模列表时可能会成为限制因素。
一个小实验:对一个包含 10 个元素的列表进行排序,结果如下:
Algorithm: bubble_sort. Minimum execution time: 0.0000909000000000014
Algorithm: insertion_sort. Minimum execution time: 0.00006681900000000268
Algorithm: quicksort. Minimum execution time: 0.0001319930000000004
结果表明:当列表足够小时,快速排序因递归开销反而比插入排序和冒泡排序更慢。
Python 中的 Timsort 算法
Timsort 被认为是一种混合排序算法,因为它巧妙地结合了插入排序和归并排序的优点。Timsort 与 Python 社区关系密切——它由 Tim Peters 于 2002 年专为 Python 语言设计,并成为 Python 的标准排序算法。
Timsort 的主要特点是:它能充分利用现实世界数据中已部分有序的子序列(称为“自然运行段”,natural runs)。算法会遍历列表,收集这些运行段,并将它们合并成一个完全有序的列表。
在 Python 中实现 Timsort
在本节中,你将实现一个简化的 Timsort,展示其核心组成部分。如果你感兴趣,也可以查阅 Timsort 的原始 C 语言实现。
首先,修改之前实现的 insertion_sort() 函数:
def insertion_sort(array, left=0, right=None):
if right is None:
right = len(array) - 1
for i in range(left + 1, right + 1):
key_item = array[i]
j = i - 1
while j >= left and array[j] > key_item:
array[j + 1] = array[j]
j -= 1
array[j + 1] = key_item
return array
这个修改版增加了 left 和 right 参数,用于指定要排序的子数组范围。这使得 Timsort 能够就地排序子数组,而无需像归并排序或快速排序那样创建新数组。
接下来是 Timsort 的实现:
def timsort(array):
min_run = 32
n = len(array)
# 第一步:将数组切分为小块(大小为 min_run),并用插入排序排序
for i in range(0, n, min_run):
insertion_sort(array, i, min((i + min_run - 1), n - 1))
# 第二步:逐步合并已排序的小块
size = min_run
while size < n:
for start in range(0, n, size * 2):
midpoint = start + size - 1
end = min((start + size * 2 - 1), (n - 1))
merged_array = merge(
left=array[start:midpoint + 1],
right=array[midpoint + 1:end + 1]
)
array[start:start + len(merged_array)] = merged_array
size *= 2
return array
实现要点总结:
- 第 8–9 行:将数组切分为大小为
min_run(默认 32)的小段,并用插入排序排序。我们知道插入排序在小数组上非常快,Timsort 正是利用了这一点。 - 第 16 行起:开始合并这些已排序的小段。初始合并大小为 32,之后每次迭代将合并块大小翻倍,直到整个数组被合并为一个有序序列。
- 与归并排序不同,Timsort 合并的是已经排好序的子数组,从而减少了比较次数,提升了效率。
为什么 min_run = 32?
- 小数组用插入排序很快,所以
min_run应该较小。若设得太大,反而会拖慢整体速度。 - 合并两个大小相近的数组效率更高。选择 32(2 的幂)有助于在后续合并阶段保持平衡。
注意:实际 Timsort 的
min_run计算更复杂。它会选择 32 到 64 之间的一个值,使得n / min_run尽可能接近 2 的幂。如果无法精确满足,则选择略小于 2 的幂的值。详情可参考 “Computing minrun” 部分的完整分析。
Timsort 的时间复杂度分析
Timsort 的平均时间复杂度为 O(n log₂n),与归并排序和快速排序相同。其中对数部分来源于每次合并操作时运行段大小的翻倍。
但 Timsort 在已排序或接近已排序的列表上表现极为出色,此时能达到 O(n) 的最佳情况。这明显优于归并排序,也与快速排序的最佳情况持平。
更重要的是,Timsort 的最坏情况也是 O(n log₂n),远优于快速排序的 O(n²)。
对你的 Timsort 实现进行计时
你可以使用 run_sorting_algorithm() 来测试 Timsort 对一万个元素数组的排序性能:
if __name__ == "__main__":
array = [randint(0, 1000) for i in range(ARRAY_LENGTH)]
run_sorting_algorithm(algorithm="timsort", array=array)
运行脚本:
$ python sorting.py
Algorithm: timsort. Minimum execution time: 0.5121690789999998
Timsort 耗时 0.51 秒,比归并排序(0.61 秒)快了约 0.1 秒(17%),虽然仍不及快速排序的 0.11 秒,但比插入排序快了惊人的 11,000%!
现在,尝试对一个已排序的列表使用这四种算法:
if __name__ == "__main__":
array = [i for i in range(ARRAY_LENGTH)] # 已排序数组
run_sorting_algorithm(algorithm="insertion_sort", array=array)
run_sorting_algorithm(algorithm="merge_sort", array=array)
run_sorting_algorithm(algorithm="quicksort", array=array)
run_sorting_algorithm(algorithm="timsort", array=array)
执行结果:
Algorithm: insertion_sort. Minimum execution time: 53.5485634999991
Algorithm: merge_sort. Minimum execution time: 0.372304601
Algorithm: quicksort. Minimum execution time: 0.24626494199999982
Algorithm: timsort. Minimum execution time: 0.23350277099999994
这次,Timsort 比归并排序快了 37%,比快速排序快了 5%,充分展现了其对已排序数据的优化能力。
Timsort 的精妙之处在于:它将两种单独使用时较慢的算法(插入排序和归并排序)结合起来,扬长避短,从而取得卓越性能。
Timsort 的优缺点分析
主要缺点:实现复杂。即使我们只实现了简化版,代码量也远超其他算法,因为它同时依赖 insertion_sort() 和 merge()。
主要优点:
- 时间复杂度稳定:无论输入结构如何,始终为 O(n log₂n),不会像快速排序那样退化到 O(n²)。
- 小数组性能优异:当数组很小时,Timsort 本质上退化为插入排序,速度极快。
- 对现实数据高度适应:现实中很多数据本身就具有部分有序性,Timsort 能充分利用这一点。
因此,对于真实应用场景(尤其是数据已有一定顺序时),Timsort 是一个极佳的选择。它的自适应性使其适用于任意长度的数组。
结论
排序是每位 Python 开发者工具箱中的必备技能。掌握不同排序算法的原理及其优化方法,能帮助你构建更快、更高效的程序!
在本教程中,你学到了:
- Python 内置
sort()背后的实现机制(即 Timsort) - 大 O 表示法的含义,以及如何用它比较算法效率
- 如何实际测量代码运行时间
- 如何在 Python 中实现五种不同的排序算法
- 各种算法的优缺点与适用场景
你还接触了递归、分治、随机化等核心算法思想。这些是解决大量算法问题的基础,将在你未来的学习和研究中反复出现。