逻辑回归，使用Python实践

分类技术是机器学习和数据挖掘应用中的重要组成部分。大约 70% 的数据科学问题属于分类问题。虽然存在大量不同类型的分类问题，但逻辑回归（Logistic Regression）是一种常见且非常有用的回归方法，特别适用于解决二分类问题。另一类分类问题是多分类（Multinomial classification），用于处理目标变量包含多个类别的情形。例如，著名的鸢尾花（IRIS）数据集就是多分类问题的经典案例。其他例子还包括对文章/博客/文档进行类别分类等。

逻辑回归可用于各种分类问题，例如垃圾邮件检测。其他典型应用还包括：糖尿病预测、判断某位客户是否会购买特定产品、客户是否会流失（churn）、用户是否会点击某个广告链接等等。

逻辑回归是最简单且最常用的机器学习算法之一，专门用于两类分类任务。它易于实现，可作为任何二分类问题的基准模型（baseline）。其基本核心概念在深度学习中也具有建设性意义。逻辑回归用于描述并估计一个二元因变量（即目标变量）与若干自变量（特征变量）之间的关系。

什么是逻辑回归？

逻辑回归是一种用于预测二分类结果的统计方法。其输出或目标变量本质上是二分的（dichotomous），即只有两种可能的类别。例如，它可以用于癌症检测问题，并计算某一事件发生的概率。

逻辑回归是线性回归的一种特殊形式，其目标变量为类别型变量（categorical）。它使用对数优势比（log of odds）作为因变量。逻辑回归通过logit 函数来预测二元事件发生的概率。

线性回归方程：

y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_n x_n

其中， $y$ 是因变量， $x_1, x_2, \dots, x_n$ 是解释变量（自变量）。

Sigmoid 函数：

\sigma(z) = \frac{1}{1 + e^{-z}}

将 Sigmoid 函数应用于线性回归：

p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \dots + \beta_n x_n)}}

逻辑回归的性质：

因变量服从伯努利分布（Bernoulli Distribution）。
参数估计采用最大似然估计（Maximum Likelihood Estimation, MLE）。
没有 R² 指标；模型拟合优度通过一致率（Concordance）、KS 统计量（KS-Statistics）等指标衡量。

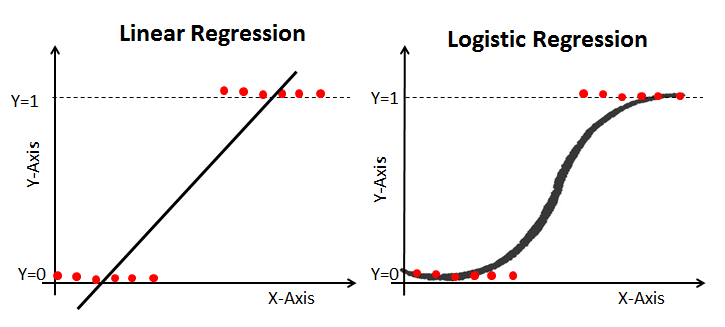
线性回归 vs. 逻辑回归

线性回归输出的是连续值，而逻辑回归输出的是离散值（类别）。例如，房价和股价是连续输出的典型例子；而预测病人是否患癌、客户是否会流失则是离散输出的例子。

逻辑回归使用最大似然估计（MLE）进行参数估计，而线性回归通常使用普通最小二乘法（Ordinary Least Squares, OLS）。当模型误差服从正态分布时，OLS 可视为 MLE 的一种特例。

最大似然估计 vs. 最小二乘法

MLE 是一种“似然”最大化方法，而 OLS 是一种最小化距离的近似方法。最大化似然函数可以确定最有可能产生观测数据的参数。从统计学角度看，MLE 将均值和方差作为参数，用于确定给定模型的具体参数值，这些参数可用于预测正态分布所需的数据。

普通最小二乘估计通过拟合一条回归线，使得所有数据点到该线的平方偏差之和最小（即最小二乘误差）。两者都用于估计线性回归模型的参数。MLE 假设联合概率质量函数，而 OLS 在最小化距离时不需要任何随机性假设。

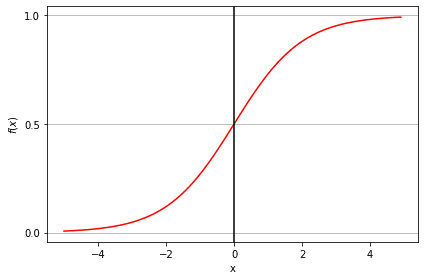
Sigmoid 函数

Sigmoid 函数（又称逻辑函数）呈现“S”形曲线，可将任意实数值映射到 0 到 1 之间的值。当输入趋向正无穷时，预测值趋近于 1；当输入趋向负无穷时，预测值趋近于 0。若 Sigmoid 函数的输出大于 0.5，则可将结果分类为 1（或 YES）；若小于 0.5，则分类为 0（或 NO）。例如，若输出为 0.75，我们可以从概率角度解释为：该患者有 75% 的可能性患有癌症。

f(x)= \frac{1}{1 + e^{-x}}

逻辑回归的类型

二元逻辑回归（Binary Logistic Regression）：目标变量仅有两个可能结果，如“垃圾邮件”或“非垃圾邮件”、“患癌”或“未患癌”。
多元逻辑回归（Multinomial Logistic Regression）：目标变量包含三个或更多无序类别，例如预测葡萄酒种类。
有序逻辑回归（Ordinal Logistic Regression）：目标变量包含三个或更多有序类别，例如餐厅或产品评分（1 到 5 星）。

使用 Scikit-learn 构建模型

下面我们使用逻辑回归分类器构建一个糖尿病预测模型。

首先，使用 pandas 的 read_csv 函数加载 Pima 印第安人糖尿病数据集。你可以从以下链接下载数据：
https://www.kaggle.com/uciml/pima-indians-diabetes-database 。

加载数据

我们通过为 pandas.read_csv() 函数提供 col_names 来简化列名。

# 导入 pandas
import pandas as pd

col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# 加载数据集
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)

pima.head()

特征选择

接下来，将给定列划分为两类变量：因变量（目标变量）和自变量（特征变量）。

# 将数据集划分为特征和目标变量
feature_cols = ['pregnant', 'insulin', 'bmi', 'age', 'glucose', 'bp', 'pedigree']
X = pima[feature_cols]  # 特征
y = pima.label          # 目标变量

数据划分

为了评估模型性能，将数据集划分为训练集和测试集是一种良好策略。

使用 train_test_split() 函数进行划分。需传入三个参数：特征、目标变量和测试集比例。此外，可使用 random_state 以确保随机选择的一致性。

# 将 X 和 y 划分为训练集和测试集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=16)

此处，数据集按 75:25 的比例划分，即 75% 用于模型训练，25% 用于模型测试。

模型开发与预测

首先导入 LogisticRegression 模块，并使用 LogisticRegression() 函数创建一个逻辑回归分类器对象（设置 random_state 以确保可复现性）。

然后，使用 fit() 方法在训练集上训练模型，并使用 predict() 方法对测试集进行预测。

# 导入模型类
from sklearn.linear_model import LogisticRegression

# 实例化模型（使用默认参数）
logreg = LogisticRegression(random_state=16)

# 使用数据拟合模型
logreg.fit(X_train, y_train)

# 进行预测
y_pred = logreg.predict(X_test)

使用混淆矩阵评估模型

混淆矩阵（Confusion Matrix）是一种用于评估分类模型性能的表格，也可用于可视化算法表现。其核心是按类别汇总正确和错误的预测数量。

# 导入评估指标类
from sklearn import metrics

cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrix

输出：

array([[115,   8],
       [ 30,  39]])

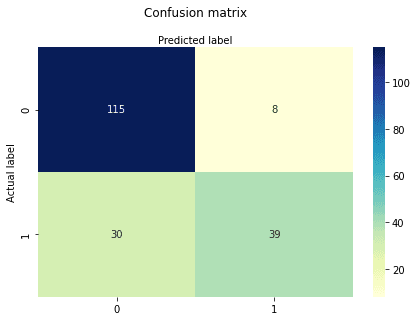
这是一个 2×2 的矩阵，因为本模型是二分类问题，只有 0 和 1 两类。对角线上的值表示正确预测，非对角线元素表示错误预测。在输出中，115 和 39 是正确预测的数量，30 和 8 是错误预测的数量。

使用热力图可视化混淆矩阵

下面使用 Matplotlib 和 Seaborn 将混淆矩阵以热力图形式可视化。

# 导入所需模块
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

class_names = [0, 1]  # 类别名称
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)

# 创建热力图
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu", fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')

# 输出标签文本
Text(0.5, 257.44, 'Predicted label')

混淆矩阵评估指标

使用 classification_report 查看准确率（accuracy）、精确率（precision）和召回率（recall）等指标。

from sklearn.metrics import classification_report

target_names = ['without diabetes', 'with diabetes']
print(classification_report(y_test, y_pred, target_names=target_names))

输出：

                   precision    recall  f1-score   support

without diabetes       0.79      0.93      0.86       123
  with diabetes        0.83      0.57      0.67        69

        accuracy                           0.80       192
       macro avg       0.81      0.75      0.77       192
    weighted avg       0.81      0.80      0.79       192

模型的分类准确率为 80%，被认为具有良好的准确性。

精确率（Precision）：指模型预测为正类的样本中，实际为正类的比例。换句话说，当模型预测某患者会患糖尿病时，有 83% 的概率是正确的。
召回率（Recall）：指在所有实际患糖尿病的患者中，模型能识别出 57%。

ROC 曲线

接收者操作特征曲线（Receiver Operating Characteristic, ROC）绘制了真正率（True Positive Rate, TPR）与假正率（False Positive Rate, FPR）之间的关系，展示了敏感性与特异性的权衡。

y_pred_proba = logreg.predict_proba(X_test)[:, 1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr, tpr, label="data 1, auc=" + str(auc))
plt.legend(loc=4)
plt.show()

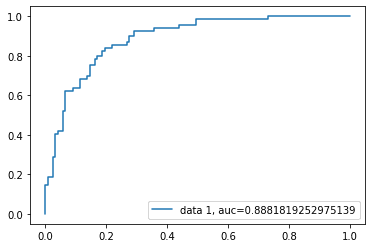
本例的 AUC 得分为 0.88。AUC 为 1 表示完美分类器，0.5 表示无分类能力的随机分类器。

优点

由于其高效且简洁的特性，逻辑回归不需要高计算资源，易于实现、易于解释，被数据分析师和科学家广泛使用。此外，它不要求对特征进行缩放，并能为每个观测提供概率得分。

缺点

逻辑回归难以处理大量类别型特征。它容易过拟合。此外，它无法解决非线性问题，因此需要对非线性特征进行变换。当自变量与目标变量不相关，或自变量之间高度相似或相关时，逻辑回归的表现会较差。

结论

在本教程中，你深入学习了逻辑回归的诸多细节：了解了什么是逻辑回归、如何构建相应模型、如何可视化结果，以及一些理论背景知识。你还掌握了 Sigmoid 函数、最大似然估计、混淆矩阵、ROC 曲线等基本概念。

希望你现在能够运用逻辑回归技术分析自己的数据集。感谢阅读本教程！